
题目列表(包括答案和解析)
7.二次函数 的部分对应值如表:
的部分对应值如表:
|
x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
y |
6 |
0 |
-4 |
-6 |
-6 |
-4 |
0 |
6 |
则不等式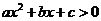 的解集为
( B
)
的解集为
( B
)
A、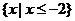 B、
B、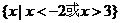 C、
C、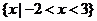 D、
D、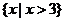
6.若集合M={0,l,2},N={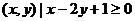 且
且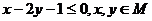 },则N中元素的个数为( C )
},则N中元素的个数为( C )
A.9 B.6 C.4 D.2
5.不等式ax2+ax-4<0的解集为R,则a的取值范围是( C )
A、-16≤a<0 B、a>-16 C、-16<a≤0 D、a<0
4.已知集合M={x|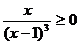 },N={y|y=3x2+1,xÎR},则MÇN=
( C )
},N={y|y=3x2+1,xÎR},则MÇN=
( C )
A、Æ B、{x|x³1} C、{x|x>1} D、{x| x³1或x<0}
3.如图I为全集,M,P,S是I的三个子集,则阴影部分所表示的集合是( C )
A 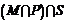 B.
B.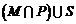 C.
C.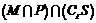 D.
D.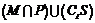
2. 若
若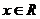 ,那么
,那么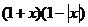 >0可化为 ( D )
>0可化为 ( D )
A.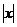 <1 B.
<1 B.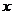 <1 C.
<1 C.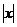 >1 D.
>1 D.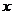 <-1或-1<
<-1或-1<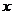 <1
<1
1.设集合 ,
,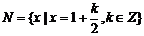 ,则( B )
,则( B )
A.M=N B.MÜN C.NÜM D.M∩N=f
20. (附加题)设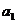 ,
,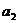 ,
, ,
, ,
,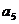 为自然数,A={
为自然数,A={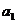 ,
,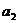 ,
, ,
, ,
,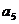 },B={
},B={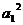 ,
,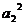 ,
,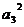 ,
,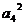 ,
,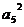 },且
},且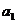 <
<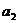 <
< <
< <
<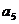 ,并满足A∩B={
,并满足A∩B={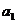 ,
, },
},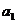 +
+ =10,A∪B中各元素之和为256,求集合A?
=10,A∪B中各元素之和为256,求集合A?
解:由A∩B={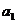 ,
, },且
},且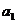 <
<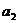 <
<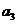 <
< <
<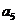 .
.
所以只可能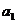 =
=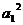 ,即
,即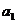 =1. 由
=1. 由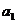 +
+ =10,得
=10,得 =9.
=9.
且 =9=
=9=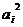 (
(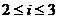 ),
),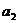 =3或
=3或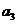 =3.
=3.
Ⅰ. =3时,
=3时,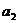 =2,此时A={1,2,3,9,
=2,此时A={1,2,3,9,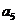 },B={1,4,9,81,
},B={1,4,9,81,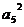 }.
}.
因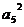
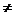
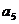 ,故1+2+3+9+4+
,故1+2+3+9+4+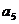 +81+
+81+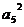 =256,从而
=256,从而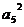 +
+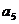 -156=0,解得
-156=0,解得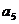 =12.略
=12.略
Ⅱ.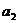 =3时,此时A={1,3,
=3时,此时A={1,3,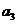 ,9,
,9,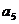 },B={1, 9,
},B={1, 9, 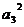 , 81,
, 81,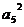 }.
}.
因1+3+9+ +
+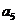 +81+
+81+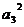 +
+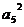 =256,从而
=256,从而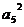 +
+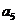 +
+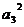 +
+ -162=0.
-162=0.
因为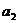 <
<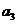 <
< ,则3<
,则3<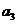 <9. 当
<9. 当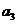 =4、6、7、8时,
=4、6、7、8时,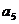 无整数解.
无整数解.
当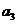 =5时,
=5时,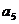 =11. 略.
=11. 略.
19. 已知命题 :
: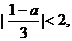 命题
命题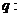 集合
集合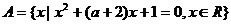 ,
,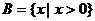 ,且
,且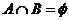 . 如果命题p且q为假命题,p或q为真命题,求实数a的取值范围.
. 如果命题p且q为假命题,p或q为真命题,求实数a的取值范围.
解:命题 为真:
为真: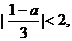 解得
解得
命题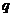 为真:(1)当
为真:(1)当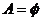 时,则
时,则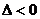 ,即
,即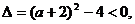 解得:
解得: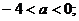
(2)当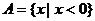 时,得
时,得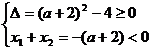 解得:
解得: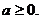
综上:a>-4
要使 真
真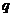 假,则
假,则 解得:
解得:
要使 假
假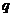 真,则
真,则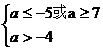 解得:
解得: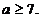
所以,实数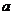 的取值范围是
的取值范围是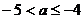 或
或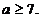
18.已知集合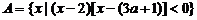 ,
,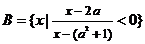 .
.
(1)当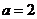 时,求
时,求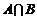 ;
;
(2)求使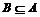 的实数
的实数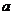 的取值范围.
的取值范围.
解:(1)当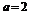 时,
时,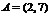 ,
,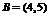 ∴
∴ 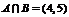 .
.
(2)∵ 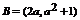 ,当
,当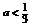 时,
时,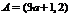 .要使
.要使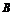
 A,必须
A,必须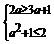 ,此时
,此时 ;
;
当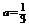 时,A=
时,A=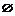 ,使
,使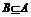 的
的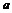 不存在;当
不存在;当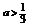 时,A=(2,3
时,A=(2,3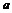 +1).要使
+1).要使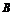
 A,必须
A,必须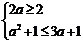 ,此时1≤
,此时1≤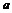 ≤3. 综上可知,使
≤3. 综上可知,使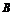
 A的实数
A的实数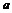 的取值范围为[1,3]∪{-1}
的取值范围为[1,3]∪{-1}
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com