(三)质疑答辩，排难解惑，发展思维．

例1．某种笔记本的单价是5元，买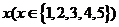个笔记本需要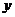元，试用三种表示法表示函数．

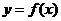分析：注意本例的设问，此处“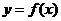”有三种含义，它可以是解析表达式，可以是图象，也可以是对应值表．

解：(略)

注意：

①函数图象既可以是连续的曲线，也可以是直线、折线、离散的点等等；

②解析法：必须注明函数的定义域；

③图象法：是否连线；

④列表法：选取的自变量要有代表性，应能反映定义域的特征．

例2．下表是某校高一(1)班三位同学在高一学年度几次数学测试的成绩及班级平均分表：

请你对这三位同学在高一学年度的数学学习情况做一个分析．

分析：本例应引导学生分析题目要求，做学情分析，具体要分析什么？怎么分析？借助什么工具？

解：(略)

注意：

①本例为了研究学生的学习情况，将离散的点用虚线连接，这样更便于研究成绩的变化特点：

②本例能否用解析法？为什么？

例3．画出函数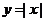的图象

解：(略)

例4．某市郊空调公共汽车的票价按下列规则制定：

(1)乘坐汽车5公里以内，票价2元；

(2)5公里以上，每增加5公里，票价增加1元(不足5公里按5公里计算)，已知两个相邻的公共汽车站间相距约为1公里，如果沿途(包括起点站和终点站)设20个汽车站，请根据题意，写出票价与里程之间的函数解析式，并画出函数的图象．

分析：本例是一个实际问题，有具体的实际意义，根据实际情况公共汽车到站才能停车，所以行车里程只能取整数值．

解：(略)

注意：

①本例具有实际背景，所以解题时应考虑其实际意义；

②象例3、例4中的函数，称为分段函数．

③分段函数的解析式不能写成几个不同的方程，而就写函数值几种不同的表达式并用一个左大括号括起来，并分别注明各部分的自变量的取值情况．

(二)研探新知

1．函数有哪些表示方法呢？

(表示函数的方法常用的有：解析法、列表法、图象法三种)

2．明确三种方法各自的特点？

(解析式的特点为：函数关系清楚，容易从自变量的值求出其对应的函数值，便于用解析式来研究函数的性质，还有利于我们求函数的值域．列表法的特点为：不通过计算就知道自变量取某些值时函数的对应值、图像法的特点是：能直观形象地表示出函数的变化情况)

(一)创设情景，揭示课题．

我们在前两节课中，已经学习了函数的定义，会求函数的值域，那么函数有哪些表示的方法呢？这一节课我们研究这一问题．

2．教学用具：圆规、三角板、投影仪．

1．学法：学生通过观察、思考、比较和概括，从而更好地完成本节课的教学目标．

教学重点：函数的三种表示方法，分段函数的概念．

教学难点：根据不同的需要选择恰当的方法表示函数，什么才算“恰当”？分段函数的表示及其图象．

3．情态与价值

让学生感受到学习函数表示的必要性，渗透数形结合思想方法。

2．过程与方法：

学习函数的表示形式，其目的不仅是研究函数的性质和应用的需要，而且是为加深理解函数概念的形成过程．

1．知识与技能

(1)明确函数的三种表示方法；

(2)会根据不同实际情境选择合适的方法表示函数；

(3)通过具体实例，了解简单的分段函数及应用．

(六)设置问题，留下悬念

1、课本P₂₈ 习题1．2(A组) 第1-7题 (B组)第1题

2、举出生活中函数的例子(三个以上)，并用集合与对应的语言来描述函数，同时说出函数的定义域、值域和对应关系。

§1．2．2函数的表示法