
题目列表(包括答案和解析)
24.(本小题满分10分)已知定义在 上的函数
上的函数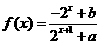 是奇函数.
是奇函数.
(1)求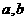 的值;
的值;
(2)若对任意的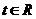 ,不等式
,不等式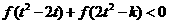 恒成立,求
恒成立,求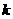 的取值范围.
的取值范围.
23. (本小题满分10分)为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为
(本小题满分10分)为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为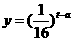 (
(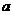 为常数),如图所示,根据图中提供的信息,解答下列问题:
为常数),如图所示,根据图中提供的信息,解答下列问题:
(1)从药物释放开始,求每立方米空气中的含药量y(毫克)
与时间t(小时)之间的函数关系式;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以
下(含0.25毫克)时,学生方可进教室,那么从药物释放开
始,至少需要经过多少小时后,学生才可以进入教室?
22.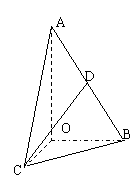 (本小题满分10分)如图,在
(本小题满分10分)如图,在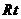 △
△ 中,
中,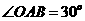 ,斜边
,斜边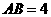 .
.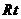 △
△ 可以通过
可以通过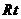 △
△ 以直线
以直线 为轴旋转得到,且二面角
为轴旋转得到,且二面角 是直二面角,
是直二面角,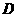 是
是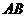 的中点.
的中点.
(1)求证: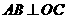 ;
;
(2)求异面直线 和
和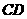 所成角的正切值.
所成角的正切值.
21.若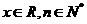 ,规定:
,规定: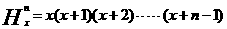 ,例如:
,例如:
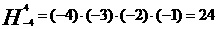 ,则
,则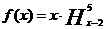 的奇偶性为(***)
的奇偶性为(***)
A.是奇函数不是偶函数 B.是偶函数不是奇函数
C.既是奇函数又是偶函数 D.既不是奇函数又不是偶函数
20.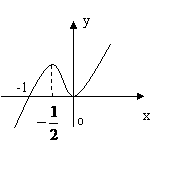 函数
函数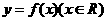 的图像如下图所示,则函数
的图像如下图所示,则函数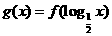 的单调递减区间是(***)
的单调递减区间是(***)
A.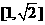 B.
B.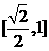
C.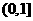 和
和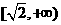 D.
D.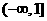 和
和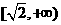
19.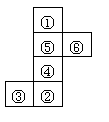
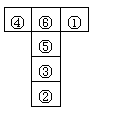
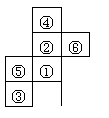
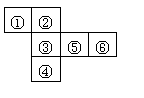 下图都是正方体的表面展开图,还原成正方体后,其中两个完全一样的是* * * (填序号).
下图都是正方体的表面展开图,还原成正方体后,其中两个完全一样的是* * * (填序号).
(1) (2) (3) (4)
18.已知函数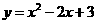 在闭区间
在闭区间 上有最大值3,最小值2,则m的取值范围是* * *.
上有最大值3,最小值2,则m的取值范围是* * *.
17.已知函数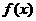 、
、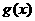 分别由下表给出:
分别由下表给出:
|
x |
1 |
2 |
3 |
|
x |
1 |
2 |
3 |
|
f (x) |
2 |
1 |
1 |
g (x) |
3 |
2 |
1 |
则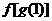 的值为 * * * ;当
的值为 * * * ;当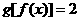 时,x = * * * .
时,x = * * * .
16.(本小题满分10分)
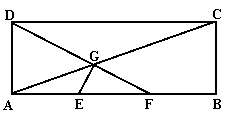 如图,在矩形ABCD中,已知AB=3, AD=1,
E、F分别是AB的两个三等分点,AC、DF相交于点G,建立适当的平面直角坐标系,证明:E G ⊥ D F.
如图,在矩形ABCD中,已知AB=3, AD=1,
E、F分别是AB的两个三等分点,AC、DF相交于点G,建立适当的平面直角坐标系,证明:E G ⊥ D F.
第II卷 共50分
15. (本题满分12分)
(本题满分12分)
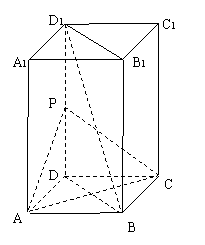
如图,长方体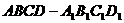 中,
中,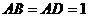 ,
,
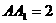 ,点
,点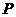 为
为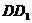 的中点.
的中点.
(1)求证:直线 ∥平面
∥平面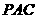 ;
;
(2)求证:平面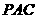
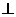 平面
平面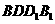 ;
;
(3)求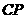 与平面
与平面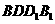 所成的角大小.
所成的角大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com