
题目列表(包括答案和解析)
24.从盛满a L(a>1)纯酒精容器里倒出1 L,然后再用水填满,再倒出1 L混合溶液后,再用水填满,如此继续下去,问第九次、第十次共倒出多少纯酒精.
23.
已知数列{an}中,a1=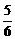 ,a2=
,a2=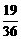 并且数列log2(a2-
并且数列log2(a2-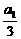 ),log2(a3-
),log2(a3-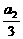 ),…,log2(an+1-
),…,log2(an+1-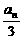 )是公差为-1的等差数列,而a2-
)是公差为-1的等差数列,而a2-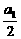 ,a3-
,a3-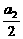 ,…,an+1-
,…,an+1-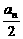 是公比为
是公比为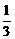 的等比数列,求数列{an}的通项公式.
的等比数列,求数列{an}的通项公式.
分析:由数列{log2(an+1-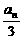 )}为等差数列及等差数列的通项公式,可求出an+1与an的一个递推关系式①;由数列{an+1-
)}为等差数列及等差数列的通项公式,可求出an+1与an的一个递推关系式①;由数列{an+1-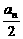 }为等比数列及等比数列的通项公式,可求出an+1与an的另一个递推关系式②.解两个关系式的方程组,即可求出an.
}为等比数列及等比数列的通项公式,可求出an+1与an的另一个递推关系式②.解两个关系式的方程组,即可求出an.
22.
数列{an}中,a1=1,an=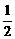 an-1+1(n≥2),求通项公式an.
an-1+1(n≥2),求通项公式an.
21.数列{an}的前n项和为Sn,数列{bn}中,b1=a1,bn=an-an-1(n≥2),若an+Sn=n.
(1)设cn=an-1,求证:数列{cn}是等比数列;
(2)求数列{bn}的通项公式.
20.等比数列{an}的各项均为正数,其前n项中,数值最大的一项是54,若该数列的前n项之和为Sn,且Sn=80,S2n=6560,求:
(1)前100项之和S100.
(2)通项公式an.
19.
已知数列{an}为等差数列,公差d≠0,{an}的部分项组成下列数列:a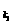 ,a
,a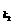 ,…,a
,…,a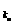 ,恰为等比数列,其中k1=1,k2=5,k3=17,求k1+k2+k3+…+kn.
,恰为等比数列,其中k1=1,k2=5,k3=17,求k1+k2+k3+…+kn.
剖析:运用等差(比)数列的定义分别求得a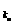 ,然后列方程求得kn.
,然后列方程求得kn.
评述:运用等差(比)数列的定义转化为关于kn的方程是解题的关键,转化时要注意:a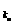 是等差数列中的第kn项,而是等比数列中的第n项.
是等差数列中的第kn项,而是等比数列中的第n项.
18. 已知等比数列{an}中,a1+a2+a3=7,a1a2a3=8,求an.
剖析:利用等比数列的基本量a1,q,根据条件求出a1和q.
评述:转化成基本量解方程是解决数列问题的基本方法.
思考讨论
用a2和q来表示其他的量好解吗?该题的{an}若成等差数列呢?
17.设数列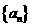 的前
的前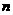 项和为
项和为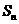 ,已知
,已知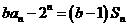
(1)证明:当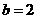 时,
时,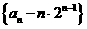 是等比数列;
是等比数列;
(2)求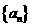 的通项公式。
的通项公式。
16. 设 、
、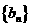 是公比不相等的两个等比数列,
是公比不相等的两个等比数列,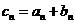 ,证明数列
,证明数列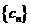 不是等比数列。
不是等比数列。
15.
已知数列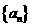 ,其中
,其中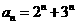 ,且数列
,且数列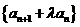 (
(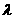 为常数)为等比数列,求常数
为常数)为等比数列,求常数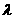 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com