
题目列表(包括答案和解析)
1.
已知角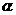 终边上一点M的坐标为
终边上一点M的坐标为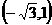 ,则
,则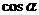 =_________________.
=_________________.
11 函数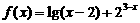 的定义域是 ****** ;
的定义域是 ****** ;
12 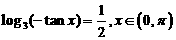 ,则
,则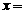 ****** (填弧度制单位的角);
****** (填弧度制单位的角);
13 教材中有这样一道题目:已知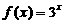 ,求证:
,求证:
(1)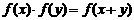 ;(2)
;(2)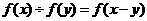 。类似地,对于幂函数,则有(1)
。类似地,对于幂函数,则有(1)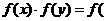 ******
******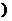 ;(2)
;(2)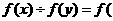 ******
******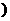 ;
;
14 下面四个命题中正确的是 ****** (把正确的命题的序号都填上)
①对于任意非空集合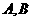 ,都有
,都有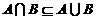 ;
;
②正弦函数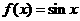 是非奇非偶函数;
是非奇非偶函数;
③对于函数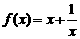 ,当
,当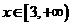 时,
时,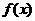 的值随着
的值随着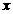 的增大而增大;
的增大而增大;
④已知函数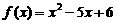 ,因为
,因为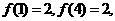 所以
所以
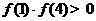 ,从而
,从而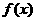 在区间
在区间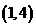 上没有零点。
上没有零点。
三 解答题(80分,将答案写在答题卷中的指定位置,要有必要的解答过程)
15.(本题满分12分)已知全集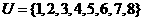 ,
,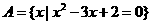 ,
,
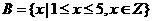 ,
,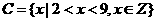 .
.
(1)求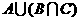 ; (2)求
; (2)求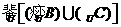 .
.
16(本题满分13分,第(1)题6分,第(2)题7分)化简或求值
(1)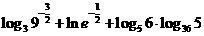
(2)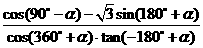
17 (本题满分13分)一次函数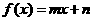 与指数型函数
与指数型函数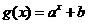 ,
,
(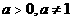 )的图像交于两点
)的图像交于两点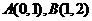 ,解答下列各题:
,解答下列各题:
(1)求一次函数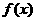 和指数型函数
和指数型函数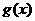 的表达式;
的表达式;
(2)作出这两个函数的图像;
(3)填空:当 ******** 时,
******** 时,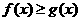 ;
;
 当
当 ********* 时,
********* 时,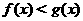 。
。
18 (本题满分13分) 2008年的金融风暴对我国的商品出口产生了较大影响,某外向型中小企业从7月份开始,所接到的订单呈现逐月减少的趋势,如果订单少于9千份,那么就会严重亏损,不得不宣布破产。已知6、7、8三个月的订单分别为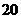 千份,
千份,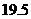 千份,
千份, 千份,若订单数
千份,若订单数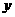 与月份
与月份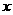 的关系接近二次函数模型,问:该企业能否坚持到12月份,不会破产?
的关系接近二次函数模型,问:该企业能否坚持到12月份,不会破产?
19 (本题满分15分)若函数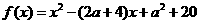 有两个不同的零点
有两个不同的零点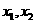 ;(1)求实数
;(1)求实数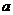 的取值范围;
的取值范围;
(2)当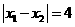 时,求
时,求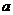 的值;
的值;
(3)记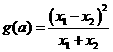 ,证明
,证明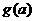 在定义域上是增函数。
在定义域上是增函数。
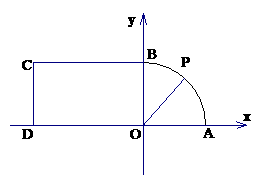 20 (本题满分14分)如图,平面直角坐标系中,由扇形
20 (本题满分14分)如图,平面直角坐标系中,由扇形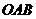 和矩形
和矩形 构成一个封闭图形,动点
构成一个封闭图形,动点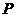 由点
由点 出发逆时针方向沿边界运动,经过点
出发逆时针方向沿边界运动,经过点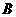 、点
、点 ,最后到达点
,最后到达点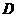 ;记
;记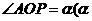 为弧度单位)。已知
为弧度单位)。已知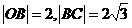 ,设点
,设点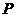 走过的路程为
走过的路程为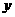 ,求解下列各题:
,求解下列各题:
(1)当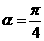 时,
时,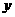 是多少?
是多少?
(2)当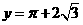 时,
时,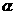 是多少?
是多少?
(3)将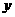 表示成
表示成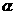 的函数。
的函数。
1 集合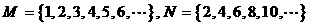 ,则
,则
A 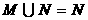 B
B 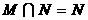 C
C 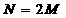 D
D 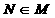
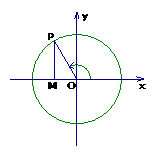 2
2 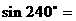
A 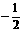 B
B 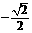 C
C 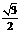 D
D 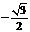
3 如图,线段 是单位圆中的角
是单位圆中的角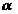 正弦线,则当
正弦线,则当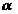 变 化时,线段
变 化时,线段 的值的变化范围是
的值的变化范围是
A 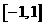 B
B 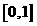 C
C 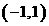 D
D 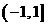
4 函数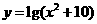 的最值的说法正确的是
的最值的说法正确的是
A 没有最值 B 有最小值1 C 有最大值1 D 有最小值0
5 第二象限角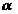 的正弦值为
的正弦值为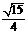 ,则正切值为
,则正切值为
A  B
B 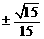 C
C  D
D 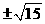
6 已知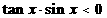 ,则
,则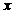 是第几象限的角?
是第几象限的角?
A 第一、二 B 第二、四 C 第二、三 D 第三、四
7 方程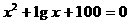 的根的情况,有四个结论,正确的结论是
的根的情况,有四个结论,正确的结论是
①无实根;②有一个实根;③有两个实根;④有一个小于1而大于0的实根
A ②④ B ① C ③ D ①②③④都不正确
 |
 |
 |
 |
1 |
2 |
3 |
 |
4 |
1 |
 |
 |
3 |
5 |
 |
1 |
4 |
2 |
3 |
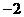 |
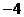 |
8 观察数表
则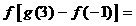
A
3
B 4 C 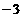 D 5
D 5
9 下列函数既是奇函数又是增函数的是
A 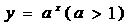 B
B 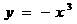
C 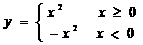 D
D 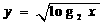
10设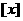 表示数
表示数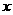 的整数部分(即小于等于
的整数部分(即小于等于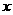 的最大整数),例如
的最大整数),例如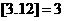 ,
,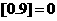 ,
,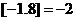 ,那么函数
,那么函数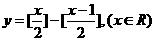 的值域为
的值域为
A. B.
B.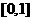 C.
C.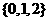 D.
D.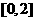
22.(本小题12分) 函数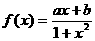 是定义在(-1,1)上的奇函数,且
是定义在(-1,1)上的奇函数,且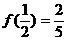
(1)确定函数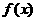 的解析式;
的解析式;
(2)用定义证明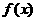 在(-1,1)上是增函数;
在(-1,1)上是增函数;
(3)求满足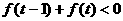 的t的取值范围。
的t的取值范围。
21.(本小题10分)对于函数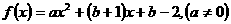 ,若存在实数
,若存在实数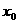 ,使
,使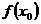 =
=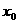 成立,则称
成立,则称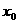 为
为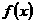 的不动点.
的不动点.
⑴当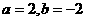 时,求
时,求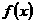 的不动点;
的不动点;
⑵若对于任意实数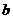 ,函数
,函数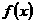 恒有两个不相同的不动点,求
恒有两个不相同的不动点,求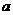 的取值范围.
的取值范围.
20. (本小题10分)如图,ABCD是正方形,O是正方形的中心,
 PO
PO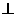 底面ABCD,E是PC的中点.
底面ABCD,E是PC的中点.
求证:(1)PA∥平面BDE;(2)平面PAC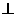 平面BDE.
平面BDE.
19.(本小题8分)某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆。每辆租出的车每月需要花费租赁公司维护费200元。
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少元?
18.(本小题8分) 已知直线l过点P(1,1), 并与直线l1:x-y+3=0和l2:2x+y-6=0分别交于点A、B,若线段AB被点P平分,求:
(1)直线l的方程; (2)以O为圆心且被l截得的弦长为 的圆的方程.
的圆的方程.
17.(本小题8分)不用计算器求下列各式的值
⑴ 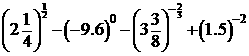 ⑵
⑵ 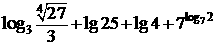
16.两圆相交于点A(1,3)、B(m,-1),两圆的圆心均在直线x-y+c=0上,则m+c的值为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com