
题目列表(包括答案和解析)
8.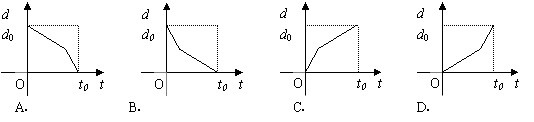 某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了再走余下的路程
某学生离家去学校,由于怕迟到,所以一开始就跑步,等跑累了再走余下的路程 在下图中纵轴表示离学校的距离,横轴表示出发后的时间,则下图中的四个图形中较符合该学生走法的是( )
在下图中纵轴表示离学校的距离,横轴表示出发后的时间,则下图中的四个图形中较符合该学生走法的是( )
3. 空间中直线与平面的位置关系有且只有( )
A.直线在平面内 B.直线与平面相交
C.直线与平面平行 D. 直线在平面内或直线与平面相交或直线与平面平行
4 长方体的一个顶点上三条棱长分别是
长方体的一个顶点上三条棱长分别是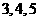 ,且它的
,且它的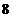 个顶点都在同一球面上,则这个球的表面积是( )
个顶点都在同一球面上,则这个球的表面积是( )
A
 B
B
 C
C
 D
D
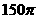
5 直线
直线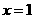 的倾斜角和斜率分别是( )
的倾斜角和斜率分别是( )
A
 B
B
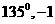
C
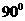 ,不存在 D
,不存在 D
 ,不存在
,不存在
6 若
若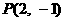 为圆
为圆 的弦
的弦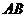 的中点,则直线
的中点,则直线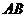 的方程是( )
的方程是( )
A
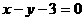 B
B
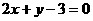
C
 D
D
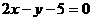
7 如果奇函数
如果奇函数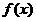 在区间
在区间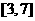 上是增函数且最大值为
上是增函数且最大值为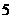 ,那么
,那么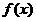 在区间
在区间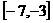 上是(
)
上是(
)
A 增函数且最小值是
增函数且最小值是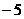 B
B 增函数且最大值是
增函数且最大值是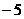
C 减函数且最大值是
减函数且最大值是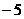 D
D 减函数且最小值是
减函数且最小值是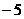
2.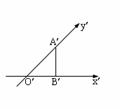 一个水平放置的三角形的斜二侧直观图是等腰直角
一个水平放置的三角形的斜二侧直观图是等腰直角
三角形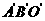 ,若
,若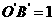 ,那么原DABO的面积是( )
,那么原DABO的面积是( )
A.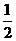 B.
B.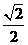 C.
C.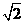 D.
D. 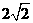
1.集合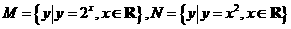 ,则
,则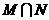 为( )
为( )
A. 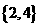 B.
B.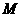 C.
C. 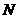 D.
D.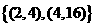
20.(本小题满分18分)
已知函数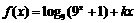 (
(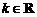 )是偶函数.
)是偶函数.
(1)求k的值;
(2)若函数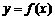 的图象与直线
的图象与直线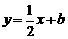 没有交点,求b的取值范围;
没有交点,求b的取值范围;
(3)设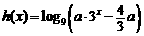 ,若函数
,若函数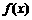 与
与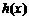 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数
a的取值范围.
19.(本小题满分18分)
已知函数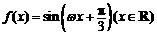 ,且
,且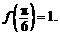
(1)求 的最小正值及此时函数
的最小正值及此时函数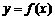 的表达式;
的表达式;
(2)将(1)中所得函数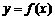 的图象结果怎样的变换可得
的图象结果怎样的变换可得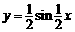 的图象;
的图象;
(3)在(1)的前提下,设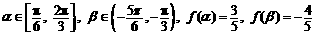 ,
,
①求 的值;
的值;
②求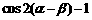 的值.
的值.
18.(本小题满分14分)
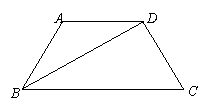 如图,在四边形ABCD中,
如图,在四边形ABCD中,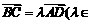 R),
R),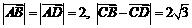 , 且
, 且
△BCD是以BC为斜边的直角三角形. 求:
(1)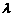 的值;
的值;
(2)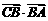 的值.
的值.
17.(本小题满分16分)
已知函数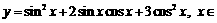 R.
R.
(1)求该函数的单调增区间;
(2)求该函数的最大值及对应的x的值;
(3)求该函数的对称轴方程与对称中心坐标.
16.(本小题满分12分)
函数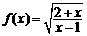 的定义域为集合A,关于x的不等式
的定义域为集合A,关于x的不等式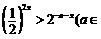 R)的解集为B,
R)的解集为B,
求使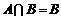 的实数a取值范围.
的实数a取值范围.
15.(本小题满分12分)
已知某皮鞋厂一天的生产成本C(元)与生产数量n(双)之间的函数关系是C=4000+50n.
若每双皮鞋的售价为90元,且生产的皮鞋全部售出. 试写出这一天的利润P关于这一
天的生产数量n的函数关系式,并求出每天至少生产多少双皮鞋,才能不亏本.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com