9．A　　　 解析：f(1，5)=f(1，4+1)=f(1，4)+2=……=f(1，1)+2×4=9. ∴(1)对，

f(5，1)=f(4+1，1)=2f(4，1)=2⁴·f(1，1)=16，(2)对.

f(5，6)=f(5，5+1)=f(5，5)+2=f(5，1)+10=16+10=26　 (3)对，故选A.

8．A　　　 解析：∵　 　∴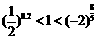

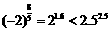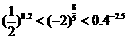
7．D　　　 解析：∵　

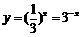
6．D　　　 解析：由定义知：A中的每一个元素在B中都可找到唯一的象与之对应，故选D.

5．C　　　 解析：分析知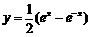在R内为奇函数，且在(0，+∞)上↑，故其反函数为奇函数，在(0，+∞)上↑

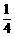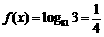4．C　　　 解析：x=2时，f(x)=2^－2=　 x=3时，，故选C.

3．B　　　 解析：f(x)=a^x+b过点(1，7)，∴a¹+b=7　 ①

又f^－1(4)=0，∴f(0)=4，∴a⁰+b=4　　　 ②　　 由①②得：a=4，b=3，故选B.

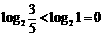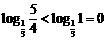
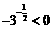
2．D　　　 解析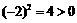：，　 　，故选D

1．C　　　 解析：P={2，3}，S={－1，2}，∴P∪S={－1，2，3}，card(P∪S)=3

21．(本小题满分14分)设函数f(x)=a^x+3a(a>0，且a≠1)的反函数为y=f^－1(x)，函数y=g(x)的图象与函数y=f^－1(x)的图象关于点(a，0)对称.

　　　 (1)求函数y=g(x)的解析式；

　　　 (2)是否存在实数a，使得当x∈[a+2，a+3]时，不等式|f^－1(x)－g(－x)|≤1恒成立？若存在，求出a的取值范围；若不存在，说明理由.