
题目列表(包括答案和解析)
19.解:任取x1、x2∈R,且x1<x2,则F(x1)-F(x2)=[f(x1)-f(a-x1)]-[f(x2)-f(a-x2)]=[f(x1)-f(x2)]+[f(a-x2)-f(a-x1)]. 由x1<x2,得a-x2<a-x1. 由f(x)是R上的增函数,得f(x1)<f(x2),f(a-x2)<f(a-x1). ∴F(x1)-F(x2)<0,即F(x1)<F(x2). 故F(x)是R上的增函数.
18.(1)x年后该城市人口总数为:y=100×(1+1%)x.
(2)2008年底该城市人口总数为:y=100×(1+1%)2=100×1.012=102.01(万人)
17.解:(1)当a=4时,原不等式等价于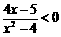 ,解得x<-2或
,解得x<-2或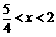 ,即集合M={x|x<-2,或
,即集合M={x|x<-2,或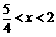 }.
}.
(2)由3∈M,得 ,解得a>9或
,解得a>9或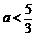 . 由5
. 由5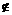 M,得
M,得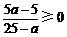 或25-a=0,解得1≤a≤25. 综上所述,所求a的取值范围为
或25-a=0,解得1≤a≤25. 综上所述,所求a的取值范围为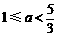 或9<a≤25.
或9<a≤25.
16.解:(1)原式=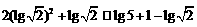
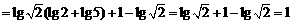
(2)由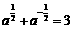 ,知
,知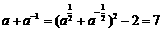

故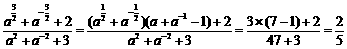
15.②④ 解析:①↓ ②中∵f(x)↓ ∴-f(x)↑ 故 ↑
↑
③f(x)↓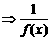 ↑
↑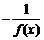 ↓ ∴
↓ ∴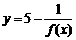 ↓
↓
④看成复合函数 y=t2和t=f(x) 在t∈(-∞,0)上y=t2↓ t=f(x)↓
∴y=[f(x)]2 ↑ 故填②④
14.(3,+∞) 解析: 的反函数为
的反函数为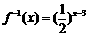 (x∈R)
(x∈R)
∴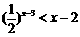 解方程
解方程 由图象可知x=3 ∴x∈(3,+∞)
由图象可知x=3 ∴x∈(3,+∞)
13.0 解析:当a=b=1时 f(1)=2f(1) f(1)=0
f(1)=0
当a=b=-1时 f(1)=-2f(-1) f(-1)=0 ∴f(-1)=0
f(-1)=0 ∴f(-1)=0
12.[-5,1] 解析:|x-1|-|2x+1|<-3
当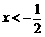 时 1-x+2x+1<-3
时 1-x+2x+1<-3 x<-5 ∴x<-5
x<-5 ∴x<-5
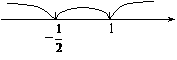
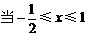 时 1-x-(2x+1)<-3
时 1-x-(2x+1)<-3 x>1 无解
x>1 无解
当x>1时 x-1-(2x+1)<-3 x>1 ∴x>1
x>1 ∴x>1
综上x<-5或x>1 ∴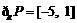
11.(0,1)∪(1,+∞) 解析:∵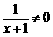 ∴y>0且y≠1.
∴y>0且y≠1.
10.A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com