
题目列表(包括答案和解析)
9.若函数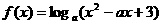 在区间
在区间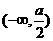 上是减函数,则
上是减函数,则 的取值范围是(
)
的取值范围是(
)
A. 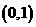 B.
B. C.
C. 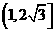 D.
D. 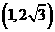
8.定义在R上的偶函数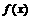 满足
满足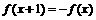 ,且当
,且当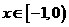 时
时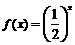 ,
,
则 等于 (
)
等于 (
)
A. 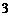 B.
B. 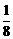 C.
C.
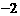 D.
D.
7.f(x)是定义在R上的奇函数,若当x∈(0,+∞)时,f(x)=lg x,则满足f(x)>0的x的取值范围是( )
A.(-1,0)∪(1,+∞)B.  C.
C. 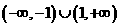 D.
D. 
6.若函数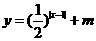 的图象与x轴有公共点,则m的取值范围是( )
的图象与x轴有公共点,则m的取值范围是( )
(A)m<0 (B)-1≤m<0 (C)m≥1 (D) 0<m≤1
5.定义集合A、B的一种运算: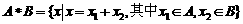 ,若
,若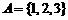 ,
,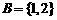 ,则
,则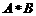 中的所有元素数字之和为( )
中的所有元素数字之和为( )
A.9 B.14 C.18 D.21
4.设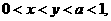 则有(
)
则有(
)
A. 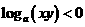 B.
B. 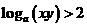
C. 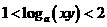 D.
D. 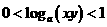
3.函数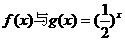 的图象关于直线
的图象关于直线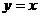 对称,则
对称,则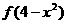 的单调增区间( )
的单调增区间( )
A.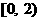 B.
B.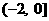 C.
C.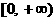 D.
D.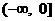
2.根据表格中的数据,可以断定方程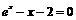 的一个根所在的区间是( )
的一个根所在的区间是( )
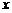 |
-1 |
0 |
1 |
2 |
3 |
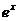 |
0.37 |
1 |
2.72 |
7.39 |
20.09 |
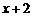 |
1 |
2 |
3 |
4 |
5 |
A. (-1,0) B. (0,1) C. (1,2) D. (2,3)
1.集合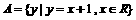 ,
,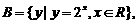 则
则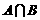 为(
)
为(
)
A.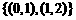 B.{0,1} C.{1,2} D.
B.{0,1} C.{1,2} D.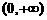
(17) (本小题满分10分)
解: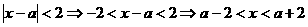 ,
,
∴ 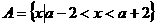 ……3分
……3分
 ,
,
∴ 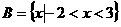 ……6分
……6分
又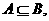
∴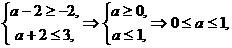
∴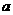 的取值范围是
的取值范围是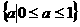 .
……10分
.
……10分
(18)(本小题满分12分)
解:(Ⅰ)令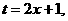 则
则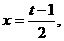 有
有
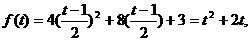
∴ 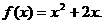 ……4分
……4分
(Ⅱ)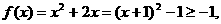
∴ 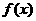 的值域为
的值域为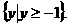 ……8分
……8分
(Ⅲ)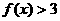 即
即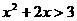 ,
,
∴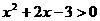 ,
,
∴ 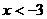 或
或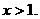 ……12分
……12分
(19)(本小题满分12分)
解:(Ⅰ)当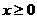 时,由
时,由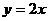 得
得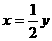 ,则
,则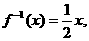
当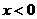 时,由
时,由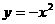 得
得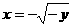 ,则
,则
 综上,
综上,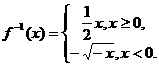 ……8分
……8分
 (Ⅱ)
(Ⅱ)
……12分
(20)(本小题满分12分)
解:①当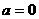 时,原不等式为
时,原不等式为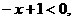
∴当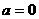 时,原不等式的解集为
时,原不等式的解集为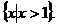 ……2分
……2分
②当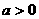 时,原不等式为
时,原不等式为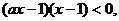
若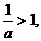 即
即 时,原不等式的解集为
时,原不等式的解集为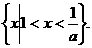 ……4分
……4分
若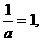 即
即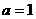 时,原不等式的解集为
时,原不等式的解集为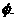 ……6分
……6分
若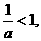 即
即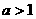 时,原不等式的解集为
时,原不等式的解集为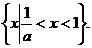 ……8分
……8分
③当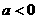 时,原不等式为
时,原不等式为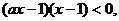
原不等式的解集为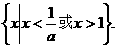 ……10分
……10分
综上,当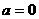 时,原不等式的解集为
时,原不等式的解集为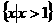 ;当
;当 时,原不等式的解集为
时,原不等式的解集为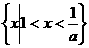 ;当
;当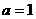 时,原不等式的解集为
时,原不等式的解集为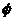 ;当
;当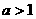 时,原不等式的解集为
时,原不等式的解集为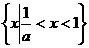 ;当
;当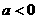 时,原不等式的解集为
时,原不等式的解集为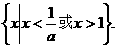 ……12分
……12分
(21)(本小题满分12分)
解:原不等式等价于
①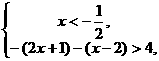 或②
或②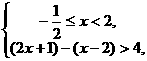 或③
或③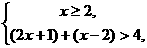
……6分
由①得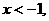
由②得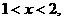
由③得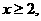
综上,原不等式的解集为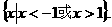 ……12分
……12分
(22)(本小题满分12分)
解:∵ 函数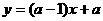 在
在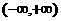 上单调递减,
上单调递减,
∴ 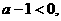 即
即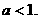
∴ 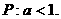 ……2分
……2分
∵ 函数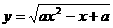 的定义域是
的定义域是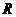 ,
,
∴ 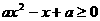 对
对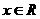 恒成立.
恒成立.
当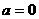 时,不符合要求.
时,不符合要求.
当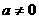 时,
时,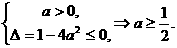
∴ 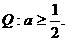 ……6分
……6分
∵ 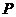 或
或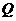 为真,
为真,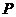 且
且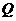 为假,
为假,
∴ 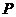 、
、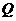 必一真一假.
……7分
必一真一假.
……7分
若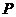 真
真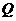 假,则
假,则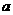 的取值范围是
的取值范围是
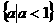 ∩
∩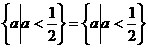 .
……9分
.
……9分
若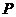 假
假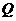 真,则
真,则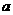 的取值范围是
的取值范围是
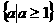 ∩
∩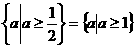 .
……11分
.
……11分
综上,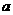 的取值范围是
的取值范围是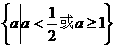 .
……12分
.
……12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com