
题目列表(包括答案和解析)
4.点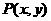 在直线
在直线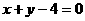 上,O是原点,则|OP|的最小值是( )
上,O是原点,则|OP|的最小值是( )
A.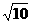 B.
B.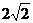 C.
C.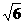 D.
D.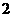
3.过点(-1,3)且垂直于直线x-2y+3=0的直线方程为( )
A.2x+y-1=0 B.2x+y-5=0
C.x+2y-5=0 D.x-2y+7=0
2.三直线ax+2y+8=0,4x+3y=10,2x-y=10相交于一点,则a的值是( )
A.-2 B.-1 C.0 D.1
1.点(0,5)到直线y=2x的距离为( )
A.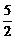 B.
B.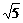 C.
C.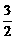 D.
D.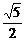
3.点P(x0,y0)到直线l:Ax+By+C=0的距离d=
两平行线l1:Ax+By+C1=0和l2:Ax+By+C2=0之间的距离d=
2.交点:
直线l1:A1x+B1y+C1=0和l2:A2x+B2y+C2=0的公共点的坐标与方程组
|
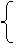 A1x+B1y+C1=0
A1x+B1y+C1=0
A2x+B2y+C2=0
相交 方程组
交点坐标就是方程组的解;
方程组
交点坐标就是方程组的解;
平行 方程组
方程组
重合 方程组
方程组
1.平行与垂直
若直线l1和l2有斜截式方程l1:y=k1x+b1,l2:y=k2x+b2,则
(1)直线l1∥l2
(2)直线l1⊥l2
若l1和l2都没有斜率,则l1与l2.
若l1和l2中有一条没有斜率而另一条斜率为0,则
(二)、基本练习:
1.过M(-2,m),N(m,4)的直线的倾斜角为90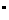 ,则m的值为( )
,则m的值为( )
A.-2 B.4 C.2 D.-4
2.点(1,3)、(5,7)和(10,12)的位置关系为( )
A.同在一条直线上 B.三点间的距离两两相等
C.三点连线组成一个直角三角形 D. 三点连线组成一个等边三角形
3.斜率为2的直线过(3,5)、(a,7)、(-1,b),则a+b等于( )
A.4 B.-7 C.1 D.-1
4.若直线(2m2+m-3)x+(m2-m)y=4m-1在x轴上的截距为1,则实数m为( )
A.1 B.2 C. 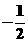 D.2或
D.2或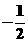
5.经过点(1,2),并且在两坐标轴上的截距的绝对值相等的直线有( )
A.1条 B.2条 C.3条 D.4条
6.直线ax+by-1=0(ab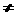 0)与两坐标轴围成的三角形的面积是( )
0)与两坐标轴围成的三角形的面积是( )
A.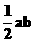 B.
B. 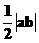 C.
C.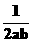 D.
D. 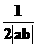
7.不论m取何值,直线(2+m)x-(1+2m)y+(1+5m)=0恒过定点_______________.
8. 已知两直线a1x+b1y+1=0和a2x+b2y+1=0的交点为P(2,3),则过两点Q1(a1,b1)、Q2(a2,b2)(a1≠a2)的直线方程为_____________________.
9.直线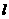 被两条直线
被两条直线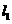 :4x+y+3=0和
:4x+y+3=0和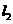 :3x─5─5=0截得的线段中点为P(─1,2),则直线
:3x─5─5=0截得的线段中点为P(─1,2),则直线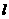 的方程为______________.
的方程为______________.
10. 已知△ABC的三个顶点是A(3,-4)、B(0,3)、C(-6,0),求它的三条边所在的直线方程.
11.已知直线l在y轴上的截距为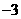 ,且它与两坐标轴围成的三角形面积为6.求直线l的方程.
,且它与两坐标轴围成的三角形面积为6.求直线l的方程.
基本练习答案:1.A 2.A 3.C 4.D 5.C 6.D 7.(1,3) 8.3x+y+1=0. 9.2x+3y+1=0.
10.解:①因为△ABC的顶点B与C的坐标分别为(0,3)和(-6,0),
故B点在y轴上,C点在x轴上,
即直线BC在x轴上的截距为-6,在y轴上的截距为3,
利用截距式,直线BC的方程为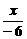 +
+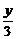 =1,
=1,
化为一般式为x-2y+6=0.
②由于B点的坐标为(0,3),故直线AB在y轴上的截距为3,利用斜截式,得直线AB的方程为y=kx+3.
又由顶点A(3,-4)在其上,所以-4=3k+3.故k=-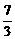 .
.
于是直线AB的方程为y=-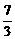 x+3,化为一般式为7x+3y-9=0.
x+3,化为一般式为7x+3y-9=0.
③由A(3,-4)、C(-6,0),
得直线AC的斜率kAC=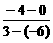 =-
=-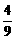 .
.
利用点斜式得直线AC的方程为
y-0=-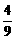 (x+6),
(x+6),
化为一般式为4x+9y+24=0.
11.解:设直线的方程为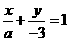 ,由题意得
,由题意得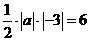 ,
,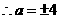 .
.
当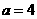 时,直线
时,直线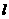 的方程为
的方程为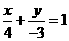 即
即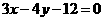 .
.
当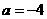 时,直线
时,直线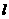 的方程为
的方程为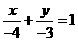 即
即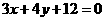 .
.
两直线位置关系
(一)、基础知识:
1.一般地,如果___________________________________,反之,______________________
__________________________________________,那么这个方程叫_________________,这条直线叫__________________.
2.经过两点A(x1,y1)、、B(x2,y2)的直线,当x1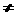 x2时,斜率k=_________,当___________时无斜率.
x2时,斜率k=_________,当___________时无斜率.
3.____________________________________叫做这条直线的倾斜角.垂直于x轴的直线的倾斜角为_________.直线的倾斜角的范围为______________.
4.直线的方程:
(1)点斜式方程:_____________________________________________________,它适用于_______________________的直线.
(2)截距式方程:_____________________________________________________,它适用于_______________________的直线.
(3)两点式方程:_____________________________________________________,它适用于_______________________的直线.
(4)一般式方程:_____________________________________________________,它适用于_______________________的直线.
(二)、基本练习:
1.若两直线a与b异面,则过a且与b垂直的平面( )
A.有且只有一个 B.至多有一个
C.有无数多个 D.一定不存在
2.若一条直线l上有两个点到平面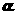 的距离相等,则l与
的距离相等,则l与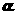 的关系是( )
的关系是( )
A.平行 B.相交 C.垂直 D.不确定
3.用一个过正四棱柱底面一边的平面去截正四棱柱,截面是( )
A.正方形 B.矩形 C.菱形 D.一般平行四边形
4.正三棱柱ABC-A1B1C1各棱长都是2,E、F分别为AB、A1C1的中点,则EF长为( )
A.2
B. C.
C.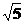 D.
D.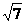 、
、
5.如果直线l、m与平面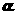 、
、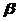 、
、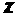 满足l=
满足l=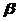
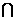
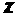 ,l//
,l//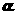 ,m
,m
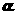 ,m
,m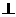
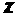 ,那么必有( )
,那么必有( )
A. 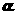
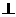
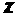 和l
和l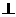 m B.
m B. 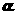 //
//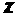 和m//
和m//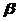
C. m//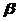 和l
和l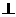 m
D.
m
D. 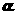 //
//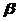 和
和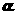
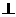
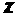
6.对两条不相交的空间直线a与b,必存在平面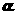 ,使得( )
,使得( )
A.a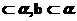 B.
B.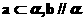
C. a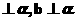 D. a
D. a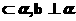
7.平面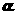 的斜线AB交
的斜线AB交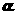 于点B,过定点A的动直线l与AB垂直,且交
于点B,过定点A的动直线l与AB垂直,且交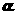 于点C,则动点C的轨迹为_____________.(填直线、圆、其它曲线)
于点C,则动点C的轨迹为_____________.(填直线、圆、其它曲线)
8.圆柱的底面半径为20,高为15,有一平行于轴且距离轴为12的截面,则这个截面的面积等于_______________.
9.长方体ABCD-A1B1C1D1中,棱AA1=5,AB=12,则直线B1C1与平面A1BCD1的距离等于________________.
10、 如图:ABCD为矩形,PA⊥平面ABCD,PA=AD,M、N、Q分别是PC、AB、CD中点,
如图:ABCD为矩形,PA⊥平面ABCD,PA=AD,M、N、Q分别是PC、AB、CD中点,
(1)求证:MN∥PAD;
(2)求证:平面QMN∥平面PAD
11、 如图,几何体ABCDE中,△ABC是正三角形,EA和DC都垂直于平面ABC,且EA=AB=2a, DC=a,F、G分别为EB和AB的中点.
如图,几何体ABCDE中,△ABC是正三角形,EA和DC都垂直于平面ABC,且EA=AB=2a, DC=a,F、G分别为EB和AB的中点.
(1)求证:FD∥平面ABC;
(2)求证:AF⊥BD;
基本练习答案:1.B 2.D 3.B 4.C 5.A 6.B 7.直线 8.480 9.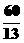
10.证明:(1)取PD的中点E,连结ME、AE
∵M、N分别是PC、PD中点
∴ME∥CD,且CD=2ME,
又AN∥CD,且CD=2AN
∴四边形ANME为平行四边形
∴MN∥AE; 又AE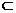 平面PAD; MN
平面PAD; MN  平面PAD
平面PAD
∴MN∥平面PAD
(2)∵M、Q分别是PC、CD中点
∴MQ∥PD, ∴QM∥平面PAD ,
又∴MN∥平面PAD(已证),MN∩MQ=M,
∴平面QMN∥平面PAD.
11.证明(1) ∵F、G分别为EB、AB的中点,
∴FG=EA,又EA、DC都垂直于面ABC, FG=DC,
∴四边形FGCD为平行四边形,∴FD∥GC,又GC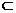 面ABC,
面ABC,
∴FD∥面ABC.
(2)∵AB=EA,且F为EB中点,∴AF⊥EB ①
又FG∥EA,EA⊥面ABC
∴FG⊥面ABC ∵G为等边△ABC,AB边的中点,∴AG⊥GC.
∴AF⊥GC又FD∥GC,∴AF⊥FD ②
由①、②知AF⊥面EBD,又BD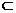 面EBD,∴AF⊥BD.
面EBD,∴AF⊥BD.
斜率与直线方程
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com