
题目列表(包括答案和解析)
6.点P在正方形ABCD所在平面外,PD⊥平面ABCD,PD=AD,则PA与BD所成角的度数为 ( )
A.30° B.45° C.60° D.90°
5.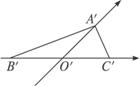 已知水平放置的△ABC是按“斜二测画法”得到如图所示的直观图,其中B′O′=C′O′=1,A′O′=
已知水平放置的△ABC是按“斜二测画法”得到如图所示的直观图,其中B′O′=C′O′=1,A′O′=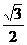 ,那么原△ABC是一个 ( )
,那么原△ABC是一个 ( )
A.等边三角形
B.直角三角形
C.三边中有两边相等的等腰三角形
D.三边互不相等的三角形
4.设 为偶函数,且
为偶函数,且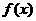 在
在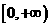 上是增函数,则
上是增函数,则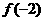 、
、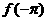 、
、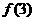 的大小顺序是( )
的大小顺序是( )
A.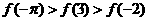 B.
B.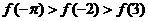
C.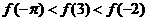 D.
D.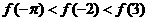
3.已知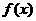 是偶函数,当x<0时,
是偶函数,当x<0时,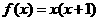 ,则当x>0时,
,则当x>0时,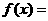 ( )
( )
A.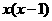 B.
B.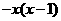 C.
C.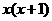 D.
D.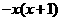
2.函数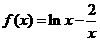 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A.(1,2)
B.(2,3)
C.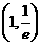 和(3,4) D.
和(3,4) D.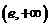
1.设全集U={1,2,3,4,5},集合A={1,2},B={2,3},则A∩CUB( )
A.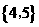 B.
B.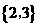 C .
C .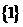 D.
D.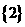
22.
(14分)通过研究学生的学习行为,心理学家发现,学生的接受能力依赖于老师引入概念和描述问题所用的时间:讲座开始时,学生兴趣激增;中间有一段不太长的时间,学生的兴趣保持较理想的状态;随后学生的注意力开始分散。分析结果和实验表明,用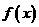 表示学生接受概念的能力(
表示学生接受概念的能力(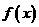 的值愈大,表示接受的能力愈强),
的值愈大,表示接受的能力愈强),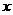 表示提出和讲授概念的时间(单位:分),可有以下的公式:
表示提出和讲授概念的时间(单位:分),可有以下的公式:
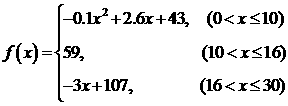 ,
,
(1)开讲后多少分钟,学生的接受能力最强?能维持多长时间?
(2)开讲后5分钟与开讲后20分钟比较,学生的接受能力何时强一些?
(3)一个数学难题需要55的接受能力及13分钟时间,老师能否在学生一直达到所需接受能力的状态下讲完这个难题?
21. (12分)设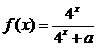 ,且
,且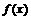 的图象过点
的图象过点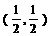 ,
,
(1)求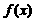 表达式,
表达式,
(2)计算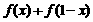 ,
,
(3)试求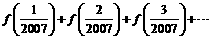
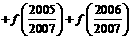 的值。
的值。
20.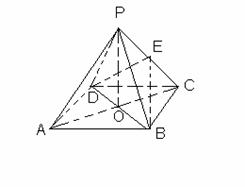 (12分)如图,ABCD是正方形,O是正方形的中心,PO
(12分)如图,ABCD是正方形,O是正方形的中心,PO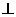 底面ABCD,E是PC的中点。
底面ABCD,E是PC的中点。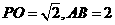
求证:(1)PA∥平面BDE
(2)平面PAC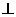 平面BDE
平面BDE
(3)求二面角E-BD-A的大小。(12分)
19.(12分)已知正方形ABCD和正方形ABEF所在的平面相交于AB,点M,N分别在AC和BF上,且AM=FN.
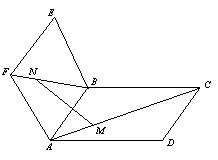 求证:MN‖平面BCE.
求证:MN‖平面BCE.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com