
题目列表(包括答案和解析)
1.下列图形符号是判断框的是( )




A. B. C. D.
20. (本小题满分10分)
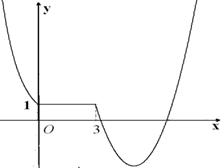
(1) 由x = 8 > 3, 且点Q在函数图象上得:
6 = ( 8 – 5 ) 2 – a , 解得a = 3.
得f ( x ) = 2分
2分
图象如图所示. 2分
(2) 由f (x ) = 9, 得 3 – x = 9或(x – 5)2 – 3 = 9,
解得: x = –
2 , 或x = 5 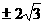 (负舍去)
(负舍去)
得 x = –
2 , 或x = 5  . 2分
. 2分
(3) 当t ≤ – 1时, q (t ) = f (t + 1 ) – f ( t ) = 3 – t – 1 – 3– t = – 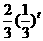 ,
,
此时, q (t )单调递增;
当– 1< t ≤ 0时, q (t ) = f (t + 1 ) – f ( t ) = 1 – 3– t = 1–  ,
,
此时, q (t )单调递增;
当0 < t ≤ 2时, q (t ) = f (t + 1 ) – f ( t ) = 1 – 1 =0, 此时, q (t )是常数函数;
当2< t ≤ 3时, q (t ) = f (t + 1 ) – f ( t ) = (t – 4 )2 – 4 , 此时, q (t )单调递减;
当3< t 时, q (t ) = f (t + 1 ) – f ( t ) = (t – 4 )2 – 3 –(t – 5 )2 + 3 = 2t - 9 , 此时, q (t )单调递增.
综合上述, 函数q (t ) 的单调递增区间是(– ∞,0]和[3, +∞]. 4分
注: 正确给出递增区间2分, 有说明2分.
19. (本小题满分10分)
(1)
由 1分
1分
所以f(x)= log2x – 1 .由条件得: n = log2Sn – 1 .
得:  ,
1分
,
1分
 ,
,
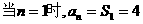 ,
,
所以 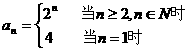 .
2分
.
2分
(2)  , 不等式成立.
1分
, 不等式成立.
1分
 bn = f(an) – 1= n – 2 ,
bn = f(an) – 1= n – 2 ,
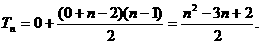
 ,
,
解得:  3分
3分
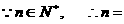 2,3 1分
2,3 1分
所求不等式的解集为{1, 2,3 }. 1分
18. (本小题满分10分)
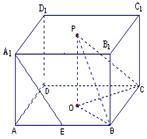
(1)∵ABCD是正方形,O为中心, ∴BO⊥OC,
∵O,P分别是正方体ABCD-A1B1C1D1底面的中心,
∴PO⊥平面ABCD, ∴PO⊥OB,
∴OB⊥平面PCO, 3分
又∵OB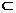 平面PBO, ∴平面PBO⊥平面PCO;
2分
平面PBO, ∴平面PBO⊥平面PCO;
2分
(2) ∵B1C1∥BC,
∴直线B1C1与平面POB所成的角等于直线BC与平面POB所成的角
∵平面PBO⊥平面PCO, OC⊥OB, ∴OC⊥平面POB,
∠CBO就是B1C1与平面POB所成的角. 3分
在△CBO中, ∠CBO =  . 所以直线B1C1与平面POB所成的角为
. 所以直线B1C1与平面POB所成的角为 . 2分
. 2分
17.(本小题满分10分)
(1) PQ的方程为 x + y – 1 = 0. 2分
PQ中点M( ,
, ) , kPQ
= – 1,
) , kPQ
= – 1,
所以圆心C所在的直线方程: y = x . 3分
(2) 由条件设圆的方程为: (x – a )2 + ( y – b )2 = 1
由圆过P,Q点得:
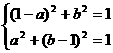 , 解得
, 解得 或
或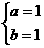
所以圆C方程为: x 2 + y 2 = 1或 x 2 + y 2 – 2x – 2y + 1 = 0. 5分
 (第18题) |
16.(本小题满分10分)
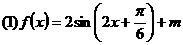
所以T = p. 5分
(2) ,
,
 时,
时,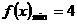 ,
,
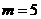 5分
5分
11. (0, 1) 12. 4n (nÎN*) 13. 2
14. 21
15.  .
.
20.(本小题满分10分)
已知函数
 图像经过点
图像经过点 .
.
(1)求 的值,并在直线坐标系中画出函数
的值,并在直线坐标系中画出函数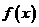 的大致图像;
的大致图像;
(2)求函数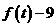 的零点;
的零点;
(3)设 ,求函数
,求函数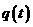 的单调递增区间。
的单调递增区间。
2009年杭州市高一年级教学质量检测
数学评分标准
19.(本小题满分10分)
已知函数 的图像经过点
的图像经过点 、点
、点 及点
及点 ,其中
,其中 为数列
为数列 的前
的前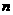 项和,
项和, 。
。
(1)求 和
和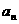 ;
;
(2)设数列 的前
的前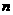 项和为
项和为 ,
, ,不等式
,不等式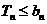 的解集,
的解集,
18.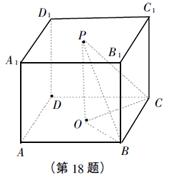 (本小题满分10分)
(本小题满分10分)
如图,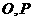 分别是正方体
分别是正方体 底面的中心,连接
底面的中心,连接
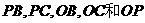 。
。
(1)求证:平面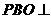 平面
平面
(2)求直线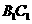 与平面
与平面 所成的角。
所成的角。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com