
题目列表(包括答案和解析)
导数的概念及其运算,利用导数研究函数的单调性和极值,函数的最大值和最小值,尤其是利用导数研究函数的单调性和极值。
11.已知函数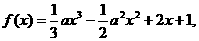 其中
其中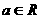 ,
,
(1)若 在
在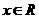 时存在极值,求
时存在极值,求 的取值范围;
的取值范围;
(2)若 在
在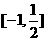 上是增函数,求
上是增函数,求 的取值范围
的取值范围
12已知函数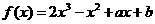 .
.
(1)若函数 的图象上有与
的图象上有与 轴平行的切线,求参数
轴平行的切线,求参数 的取值范围;
的取值范围;
(2)若函数 在
在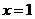 处取得极值,且
处取得极值,且 时,
时,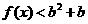 恒成立,求参数
恒成立,求参数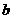 的取值范围.
的取值范围.
2.设函数 ,
, .
.
(1)当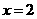 时,
时, 取得极值,求
取得极值,求 的值;
的值;
(2)若 在
在 内为增函数,求
内为增函数,求 的取值范围.
的取值范围.
3已知函数
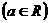
(1)若 在
在 上是减函数,求
上是减函数,求 的最大值;(2)若
的最大值;(2)若 的单调递减区间是
的单调递减区间是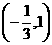 ,求函数y=
,求函数y= 图像过点
图像过点 的切线与两坐标轴围成图形的面积。
的切线与两坐标轴围成图形的面积。
4已知函数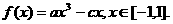
(1)若a=4,c=3,求证:对任意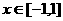 ,恒有
,恒有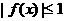 ;
;
(2)若对任意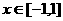 ,恒有
,恒有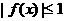 ,求证:|a|≤4.
,求证:|a|≤4.
5已知函数 的图象是曲线
的图象是曲线 ,直线
,直线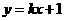 与曲线
与曲线 相切于点(1,3).
相切于点(1,3).
(1)求函数 的解析式;(2)求函数
的解析式;(2)求函数 的递增区间;
的递增区间;
(3)求函数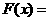
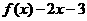 在区间
在区间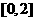 上的最大值和最小值.
上的最大值和最小值.
6用总长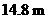 的钢条制作一个长方体容器的框架,如果容器底面的长比宽多
的钢条制作一个长方体容器的框架,如果容器底面的长比宽多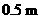 ,那么长和宽分别为多少时容器的容积最大?并求出它的最大容积 .
,那么长和宽分别为多少时容器的容积最大?并求出它的最大容积 .
7函数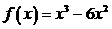 的定义域为
的定义域为 ,设
,设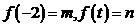 .
.

(1)求证: ;
;
(2)确定t的范围使函数 在
在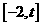 上是单调函数;
上是单调函数;
(3)求证:对于任意的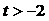 ,总存在
,总存在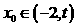 ,满足
,满足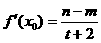 ;并确定
;并确定
这样的 的个数.
的个数.
8定义在定义域D内的函数y=f(x),若对任意的x1 、x2 ∈D,都有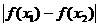 <1,则称函数y=f(x)为“Storm函数”.已知函数f(x)=x3-x+a (x∈[-1,1],a∈R).
<1,则称函数y=f(x)为“Storm函数”.已知函数f(x)=x3-x+a (x∈[-1,1],a∈R).
(1)当a=2时,求过点(1,2)处的切线方程.
(2)函数f(x)是否为“Storm函数”?如果是,请给出证明;如果不是,请说明理由.
9已知函数 的图象上点P(1,-2)处的切线方程为
的图象上点P(1,-2)处的切线方程为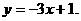
(1)若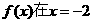 时有极值,求
时有极值,求 的表达式;
的表达式;
(2)若 在区间[-2,0]上单调递增,求实数b的取值范围.
在区间[-2,0]上单调递增,求实数b的取值范围.
10某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划建成一个矩形的高
科技工业园区.已知AB⊥BC,OA//BC,且AB=BC=4 AO=2km,曲线段OC是以点O为顶点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落在AB,BC上,且一个顶点落在曲线段OC上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到0.1km2).
1.函数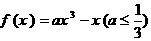
(1)若函数 在
在 时取到极值,求实数
时取到极值,求实数 得值;
得值;
(2)求函数 在闭区间
在闭区间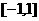 上的最大值.
上的最大值.
28.
解:(I)如图,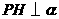 ,
, ,
,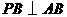 ,
,
由三垂线定理逆定理知,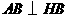 ,所以
,所以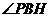 是
是
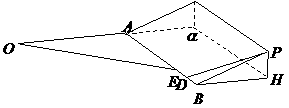 山坡与
山坡与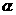 所成二面角的平面角,则
所成二面角的平面角,则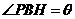 ,
,
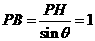 .
.
设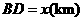 ,
, .则
.则
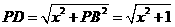
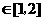 .
.
记总造价为 万元,
万元,
据题设有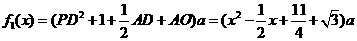

当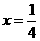 ,即
,即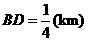 时,总造价
时,总造价 最小.
最小.
(II)设 ,
,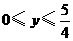 ,总造价为
,总造价为 万元,根据题设有
万元,根据题设有
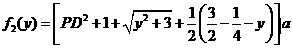
 .
.
则 ,由
,由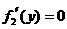 ,得
,得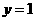 .
.
当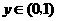 时,
时,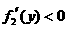 ,
, 在
在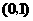 内是减函数;
内是减函数;
当 时,
时, ,
, 在
在 内是增函数.
内是增函数.
故当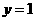 ,即
,即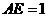 (km)时总造价
(km)时总造价 最小,且最小总造价为
最小,且最小总造价为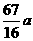 万元.
万元.
(III)解法一:不存在这样的点 ,
,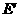 .
.
事实上,在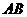 上任取不同的两点
上任取不同的两点 ,
,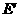 .为使总造价最小,
.为使总造价最小,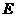 显然不能位于
显然不能位于 与
与 之间.故可设
之间.故可设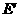 位于
位于 与
与 之间,且
之间,且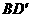 =
=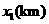 ,
,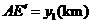 ,
,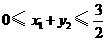 ,总造价为
,总造价为 万元,则
万元,则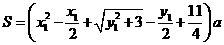 .类似于(I)、(II)讨论知,
.类似于(I)、(II)讨论知, ,
, ,当且仅当
,当且仅当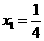 ,
,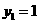 同时成立时,上述两个不等式等号同时成立,此时
同时成立时,上述两个不等式等号同时成立,此时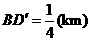 ,
, ,
, 取得最小值
取得最小值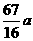 ,点
,点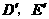 分别与点
分别与点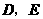 重合,所以不存在这样的点
重合,所以不存在这样的点
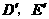 ,使沿折线
,使沿折线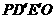 修建公路的总造价小于(II)中得到的最小总造价.
修建公路的总造价小于(II)中得到的最小总造价.
解法二:同解法一得
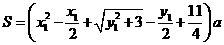
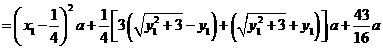
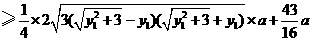
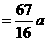 .
.
当且仅当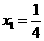 且
且 ,即
,即 同时成立时,
同时成立时, 取得最小值
取得最小值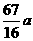 ,以上同解法一.
,以上同解法一.
本资料由《七彩教育网》 提供!
27. 本小题主要考查二次函数、二次方程的基本性质及二次不等式的解法,考查推理和运算能力.
解法1:(Ⅰ)令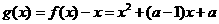 ,
,
则由题意可得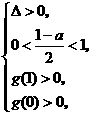

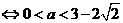 .
.
故所求实数 的取值范围是
的取值范围是 .
.
(II) ,令
,令 .
.
 当
当 时,
时,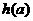 单调增加,
单调增加, 当
当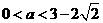 时,
时,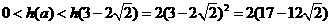
 ,即
,即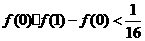 .
.
解法2:(I)同解法1.
(II)
 ,由(I)知
,由(I)知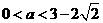 ,
,
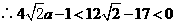 .又
.又 于是
于是
 ,
,
即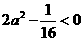 ,故
,故 .
.
解法3:(I)方程

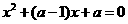 ,由韦达定理得
,由韦达定理得
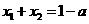 ,
,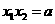 ,于是
,于是
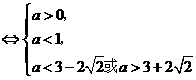
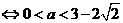 .
.
故所求实数 的取值范围是
的取值范围是 .
.
(II)依题意可设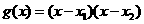 ,则由
,则由 ,得
,得
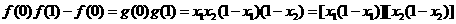
 ,故
,故 .
.
26.本小题主要考查函数、不等式和导数的应用等知识,考查综合运用数学知识解决问题的能力.
解:(Ⅰ)设 与
与 在公共点
在公共点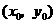 处的切线相同.
处的切线相同.
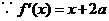 ,
, ,由题意
,由题意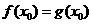 ,
,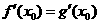 .
.
即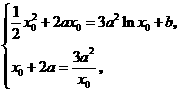 由
由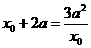 得:
得: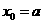 ,或
,或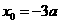 (舍去).
(舍去).
即有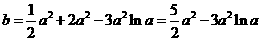 .
.
令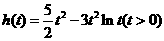 ,则
,则 .于是
.于是
当 ,即
,即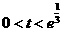 时,
时,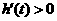 ;
;
当 ,即
,即 时,
时,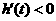 .
.
故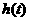 在
在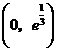 为增函数,在
为增函数,在 为减函数,
为减函数,
于是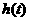 在
在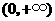 的最大值为
的最大值为 .
.
(Ⅱ)设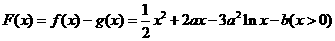 ,
,
则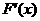
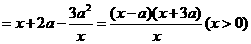 .
.
故 在
在 为减函数,在
为减函数,在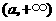 为增函数,
为增函数,
于是函数 在
在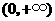 上的最小值是
上的最小值是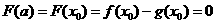 .
.
故当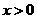 时,有
时,有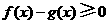 ,即当
,即当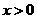 时,
时, .
.
25. 解: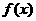 的定义域为
的定义域为 .
.
(Ⅰ) .
.
当 时,
时,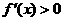 ;当
;当 时,
时,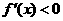 ;当
;当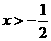 时,
时,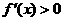 .
.
从而,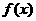 分别在区间
分别在区间 ,
,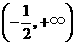 单调增加,在区间
单调增加,在区间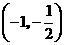 单调减少.
单调减少.
(Ⅱ)由(Ⅰ)知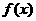 在区间
在区间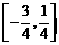 的最小值为
的最小值为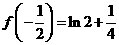 .
.
又
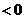 .
.
所以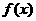 在区间
在区间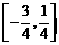 的最大值为
的最大值为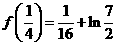 .
.
24. 解:(Ⅰ) ,
,
依题意有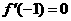 ,故
,故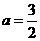 .
.
从而 .
.
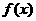 的定义域为
的定义域为 ,当
,当 时,
时,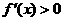 ;
;
当 时,
时,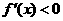 ;
;
当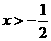 时,
时,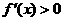 .
.
从而,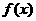 分别在区间
分别在区间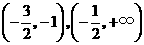 单调增加,在区间
单调增加,在区间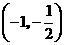 单调减少.
单调减少.
(Ⅱ)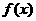 的定义域为
的定义域为 ,
,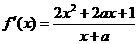 .
.
方程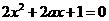 的判别式
的判别式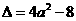 .
.
(ⅰ)若 ,即
,即 ,在
,在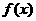 的定义域内
的定义域内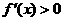 ,故
,故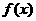 的极值.
的极值.
(ⅱ)若 ,则
,则 或
或 .
.
若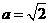 ,
,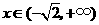 ,
, .
.
当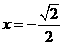 时,
时, ,当
,当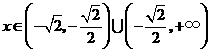 时,
时,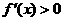 ,所以
,所以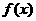 无极值.
无极值.
若 ,
, ,
,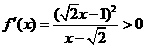 ,
,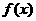 也无极值.
也无极值.
(ⅲ)若 ,即
,即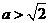 或
或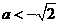 ,则
,则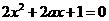 有两个不同的实根
有两个不同的实根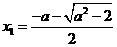 ,
,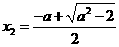 .
.
当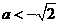 时,
时, ,从而
,从而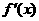 有
有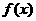 的定义域内没有零点,故
的定义域内没有零点,故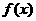 无极值.
无极值.
当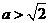 时,
时, ,
,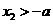 ,
,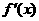 在
在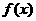 的定义域内有两个不同的零点,由根值判别方法知
的定义域内有两个不同的零点,由根值判别方法知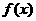 在
在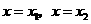 取得极值.
取得极值.
综上,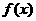 存在极值时,
存在极值时, 的取值范围为
的取值范围为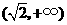 .
.
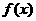 的极值之和为
的极值之和为
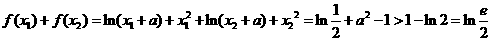 .
.
23.
解: 若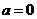 ,
, 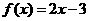 ,显然在上没有零点, 所以
,显然在上没有零点, 所以 
令  得
得 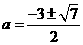
当 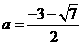 时,
时,  恰有一个零点在
恰有一个零点在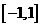 上;
上;
当 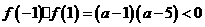 即
即 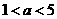 时,
时,  也恰有一个零点在
也恰有一个零点在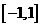 上;
上;
当  在
在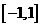 上有两个零点时, 则
上有两个零点时, 则
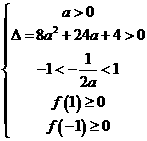 或
或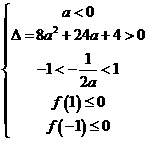
解得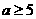 或
或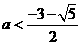
因此 的取值范围是
的取值范围是  或
或 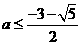 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com