
题目列表(包括答案和解析)
22、①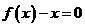
令
因为 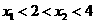 ,
,
所以

(解法1)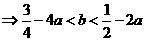
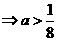
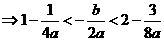

(解法2) 得
得
所以
②
 ,即
,即 同号
同号
因为
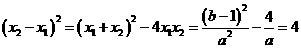
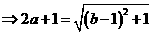
又因为
所以 
21、(Ⅰ)证明:
∵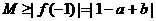


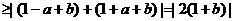 =2|1+b|
=2|1+b|
∴
(Ⅱ)证明:依题意, ,
,
又:


∴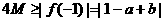
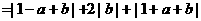

∴
20、解:
(Ⅰ)



(Ⅱ)令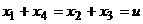 则
则
研究:

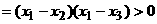
这个由于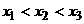 的缘故。
的缘故。
所以
(Ⅲ)研究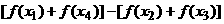
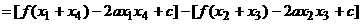
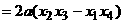
因此 当a>0时,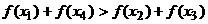
当a<0时,
19、解:(1)若买16张卡,则每位学生应交的钱数是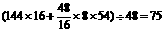 元。
元。
(2)设应该设购买x张游泳卡, 本次活动总开支为y(元),
由题意: ,
,
当且仅当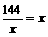 , 即x=12时取等号。3456÷48=72(元)
, 即x=12时取等号。3456÷48=72(元)
答:买12张游泳卡最合算,每人只需交72元。
18、当 时,由已知不等式得
时,由已知不等式得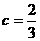
下面分两部分给出证明:
⑴先证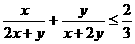 ,
,
此不等式
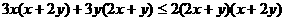
 ,此式显然成立;
,此式显然成立;
⑵再证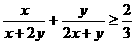 ,
,
此不等式
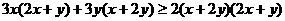
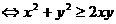 ,此式显然成立.
,此式显然成立.
综上可知,存在常数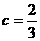 ,是对任意的整数x、y,题中的不等式成立.
,是对任意的整数x、y,题中的不等式成立.
17、原不等式等价于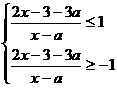 ,
,
移项,通分得
由已知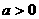 ,所以解①得
,所以解①得 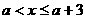 ,
,
解②得 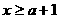 或
或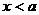
故原不等式的解集为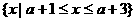
22、已知二次函数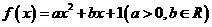 ,设方程
,设方程 有两个实数根
有两个实数根 。
。
①如果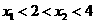 ,设函数
,设函数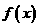 的对称轴为
的对称轴为 ,求证:
,求证: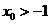 ;
;
②如果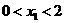 ,且
,且 的两实根的差为2,求实数
的两实根的差为2,求实数 的取值范围。
的取值范围。
答案:BDBBA DCCCB CC
> ,11-n ,n+9 ,4 ,两个等号不能同时取到
21、已知二次函数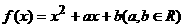 的定义域为[-1,1],
的定义域为[-1,1],
且|f(x)|的最大值为M。
(Ⅰ)试证明 ;
;
(Ⅱ)试证明 ;
;
20、设二次函数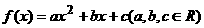
若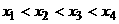 且
且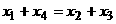
(Ⅰ)试证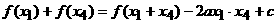
(Ⅱ)试比较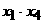 与
与 之间的大小关系。
之间的大小关系。
(Ⅲ)试比较 与
与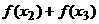 之间的大小关系。
之间的大小关系。
19、某游泳馆出售冬季学生游泳卡, 每张144元, 使用规定: 不记名, 每卡每次只限1人, 每天只限1次, 某班有48名同学, 老师打算组织同学们分组集体去游泳, 除需购买若干张游泳卡外,每次游泳还要包一辆汽车, 无论乘坐多少名同学, 每次的包车费均为54元,若使每位同学游8次。
(1) 如果买16张卡,那么每位学生需交多少钱;
(2) 买多少张游泳卡最合算(即每位同学交钱最少)?每位同学需交多少钱?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com