
题目列表(包括答案和解析)
1.设 则复数
则复数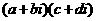 为实数的充要条件是( )
为实数的充要条件是( )
(A) (B)
(B) (C)
(C)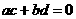 (D)
(D)
28.设复数 ,试求m取何值时
,试求m取何值时
(1)Z是实数; (2)Z是纯虚数; (3)Z对应的点位于复平面的第一象限
27.已知关于 的方程组
的方程组 有实数,求
有实数,求 的值。
的值。
26.已知复数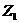 ,
, 满足
满足 ,且
,且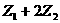 为纯虚数,求证:
为纯虚数,求证: 为实数。
为实数。
4. 线
线 上一点Q引直线
上一点Q引直线 的垂线,垂足为N,求线段QN的中点P的轨迹方程。
的垂线,垂足为N,求线段QN的中点P的轨迹方程。
答案:
2.线C∶x2+4y2=4关于直线y=x-3对称的曲线C′的方程.
由教师引导方法,学生演板完成.解答为:
设(x′,y′)是曲线C上任意一点,且设它关于直线y=x-3的对称点为(x,y).
则
又(x′,y′)为曲线C上的点,
∴(y+3)2+4(x-3)2=4.
∴曲线C的方程为:4(x-3)2+(y+3)2=4.
3 (课本P53,习题)弦中点轨迹问题
[解](1)设这组平行直线的直线方程为y= 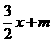 , 由
, 由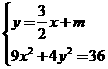 消去y,得
消去y,得
9x2+6mx+2m2 – 18 =0, 因为直线与椭圆有两个不同的交点,故△>0 Û
m Î ( ).
).
(2) 设平行直线与椭圆交点为A(x1,y1),B(x2,y2), AB中点为M(x,y)
则x = 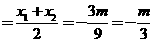 , y =
, y = 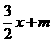 =
= ,消去m,得3x+2y=0
,消去m,得3x+2y=0
所以这组平行弦的中点都在直线3x+2y上.
1.是双曲线 的两个焦点,Q是双曲线上任意一点,从
的两个焦点,Q是双曲线上任意一点,从 引
引 的平分线的垂线,垂足为P,则点P的轨迹方程是____________(
的平分线的垂线,垂足为P,则点P的轨迹方程是____________( )
)
5、向量工具“自觉用”
向量是新课改后增加的内容,它是数形转化的纽带,它在初等数学的各个分支中起着十分重要的工具作用,在复习时应加强训练, 并能运用自如。
典型例题
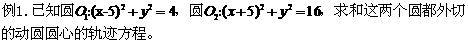

 解:圆圆心为M(x,y),半径为r
解:圆圆心为M(x,y),半径为r
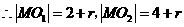 ,
,
∴M的轨迹是以O1(5,0)、 O2 (-5,0)为焦点的双曲线的右支

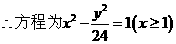
例2 设F(1,0),M点在x轴上,P点在y轴上,且 当点P在y轴上运动时,求N点的轨迹C的方程.
当点P在y轴上运动时,求N点的轨迹C的方程.
[解]∵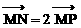 ,故P为MN中点.
,故P为MN中点.
又∵ ,P在y轴上,F为(1,0),故M在x轴的负方向上,设N(x,y)则M(-x,0),
,P在y轴上,F为(1,0),故M在x轴的负方向上,设N(x,y)则M(-x,0),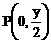 ,(x>0),
,(x>0),
∴ ,
,
又∵ 故
故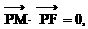
即  是轨迹C的方程。
是轨迹C的方程。
评:本题为直接法求轨迹方程.
例3. 的两个顶点B(-2,0),C(2,0),顶点A 在抛物线
的两个顶点B(-2,0),C(2,0),顶点A 在抛物线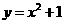 上移动,求
上移动,求 的重心的轨迹方程。
的重心的轨迹方程。
[解]设 的重心G为(x, y), A(x0, y0)
的重心G为(x, y), A(x0, y0)
则由重心坐标公式有x= 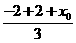 , y=
, y=
即x0 = 3x, y0 = 3y
∵顶点A 在抛物线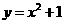 上移动
上移动
∴ Û 3y = (3x)2 +1 ,即
Û 3y = (3x)2 +1 ,即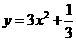
∴所求轨迹方程为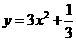 .
.
评:本题为相关点法求轨迹方程,最后求出的轨迹可以保证A,B,C不共线,所以对x, y不需要注上任何范围.
例4 已知椭圆: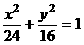 ,直线
,直线 ,P是
,P是 上一点,射线OP交椭圆于一点R,点Q在OP上且满足
上一点,射线OP交椭圆于一点R,点Q在OP上且满足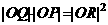 ,当点P在
,当点P在 上移动时,求点Q的轨迹方程,并说明轨迹是什么曲线?
上移动时,求点Q的轨迹方程,并说明轨迹是什么曲线?
 [解]如图2,显然点Q在椭圆内,因
[解]如图2,显然点Q在椭圆内,因 共线。故可设
共线。故可设 ,l>0, m>0, 设Q(x, y),则
,l>0, m>0, 设Q(x, y),则
 ,
, ,
,

由 ,得
,得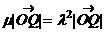

 ,
,
 点R在椭圆上,点P在
点R在椭圆上,点P在 上,
上,

 即
即
 整理得
整理得
评: 本题为双参数法求轨迹方程.
 例5.已知两点
例5.已知两点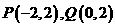 以及一条直线
以及一条直线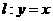 ,设长为
,设长为 的线段AB在直线
的线段AB在直线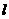 上移动,求直线PA和QB的交点M的轨迹方程。
上移动,求直线PA和QB的交点M的轨迹方程。

|
|
则由|AB|= Þ b = a+1
Þ b = a+1
|
|

直线QB方程为y – 2 = 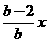
∴动点M满足 ,消去参数a, b得
,消去参数a, b得 .
.
评:本题为参数法求轨迹方程,属于交轨问题(交点轨迹问题),常见题型.
例6.设椭圆方程为 ,过点
,过点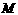 (0,1)的直线
(0,1)的直线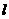 交椭圆于点
交椭圆于点 、
、 是坐标原点,点
是坐标原点,点 满足
满足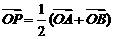 ,点
,点 的坐标为
的坐标为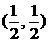 ,当
,当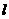 绕点
绕点 旋转时,求:
旋转时,求:
(1)动点 的轨迹方程; (2)
的轨迹方程; (2) 的最小值与最大值.
的最小值与最大值.
解. 直线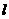 过点
过点 (0,1), 斜率存在时设其为
(0,1), 斜率存在时设其为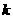 ,则
,则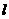 的方程为
的方程为
由方程组 消元得
消元得 ,记
,记 、
、
则有  于是
于是 =
=
设点 的坐标为
的坐标为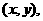 则
则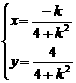 消去参数
消去参数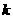 得
得 .* 当
.* 当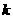 不存在时,
不存在时,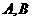 中点为坐标原点(0,0),也满足方程*,所以点
中点为坐标原点(0,0),也满足方程*,所以点 的轨迹方程为
的轨迹方程为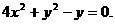
(2)由点 的轨迹方程知
的轨迹方程知 , 即
, 即 ,
,
所以 ,
,
故当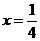 时,
时, 取得最小值为
取得最小值为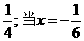 时,
时, 取得最大值为
取得最大值为 .
.
例7.(辽宁2008)直角坐标系 中,点P到两点
中,点P到两点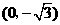 ,
,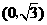 的距离之和等于
的距离之和等于
4,设点P的轨迹为 ,直线
,直线 与C交于A,B两点.
与C交于A,B两点.
(Ⅰ)写出C的方程;
(Ⅱ)若
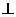
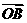 ,求k的值;
,求k的值;
(Ⅲ)若点A在第一象限,证明:当k>0时,恒有| |>|
|>|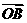 |.
|.
解:(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以 为焦点,长半轴为2的椭圆.它的短半轴
为焦点,长半轴为2的椭圆.它的短半轴 ,
,
故曲线C的方程为 .
.
(Ⅱ)设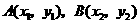 ,其坐标满足
,其坐标满足
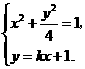
消去y并整理得 ,
,
故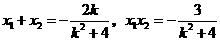 .
.
若 ,即
,即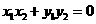 .
.
而 ,
,
于是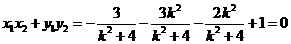 ,
,
化简得 ,所以
,所以 .
.
(Ⅲ)
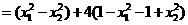
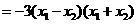
 .
.
因为A在第一象限,故 .由
.由 知
知 ,从而
,从而 .又
.又 ,
,
故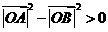 ,
,
即在题设条件下,恒有 .
.
练习
4、平几知识“首先用”
在处理轨迹问题时, 要特别注意运用平面几何知识, 其作用主要有:①题中没有给出明显的条件式时,可帮助列式;②简化条件;③可以等价转化问题。
3、认真细致定范围
确定轨迹的范围是处理轨迹问题的难点,也是容易出现错误的地方,在确定轨迹范围时,应注意以下几个方面:①准确理解题意,挖掘隐含条件;②列式不改变题意,并且要全面考虑各种情形;③推理要严密,方程化简要等价;④消参时要保持范围的等价性;⑤数形结合,查“漏”补“缺”。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com