6、解答：件，

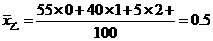件，由于工人乙平均每天出次品0.5件，低于甲，所以按题意要求应确定乙升任工长．

[拓展探究]

解答：(1)根据题意，甲两次购粮分别用去元、元，乙两次购粮的数量为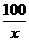(千克)和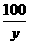(千克)，所以甲两次购粮的平均单价为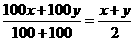，乙两次购粮的平均单价为 ．

(2)，又，，．

又由已知，．， ．

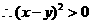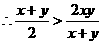答：乙两次购粮的平均单价比较低．

[回顾反思]

一组数据的平均数为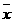，则一组新数据的平均数为　　　　

第9课时

[范例展示]

例1、解答：(1)，

．

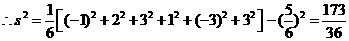(2)方法一，用简化公式：

取，则有，

．

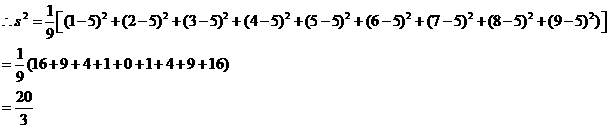方法二，用新数据法：取，则有，　　　　 例2、解答：取，取得新数据：，，，，5，，，，．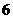

，

，

．

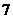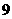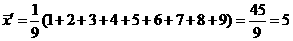[自我测评]

1、C　 2、B　 3、D　 4、10　 5、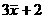　

6、解答：班级平均得分

分．

答：该班平均得分3.4分．

[拓展探究]

解答：设甲地到乙地路程为，则根据题意，得

(米/秒)

[回顾反思]

第8课时

[范例展示]

例1、分析：利用方程的思想，设立未知数，用平均数公式列方程组求解．

解答：设投进3个球的人数为，投进4个球的人数为，则由平均数的意义，可得

即解得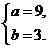

答：投进3个球的人数为9人，投进4个球的人数为3人．

评析：本题实质上考查平均数的概念及计算公式，应用平均数公式得到关系式，转化为方程组问题求解． 例2、分析：首先应计算出样本的平均数，然后用样本的平均数去估计总体的平均数，从而计算出总产量、总收入，进而求出纯收入．

解答：(1)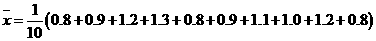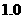＝(千克)，

(千克)．

(2)(元)，5600016000=40000(元)．

(3)设平均每年的增长率为，根据题意得，

，解得(舍去)，

所以增长率为10%．

评析：由于鱼在池塘中，无法精确计算其重量，只有用样本平均数去估计总体平均数，再由成活率，则可以估计池塘中的鱼的总量．

[自我测评]

1、C 2、D 3、A 4、C 5、

12．要分析学生初中升学的数学成绩对高一年级数学学习有什么影响，在高一年级学生中随机抽选名学生，分析他们入学的数学成绩()和高一年级期末数学考试成绩()(如下表)：

编号	1	2	3	4	5	6	7	8	9	10
	63	67	45	88	81	71	52	99	58	76
	65	78	52	82	92	89	73	98	56	75

画出散点图；

对变量和进行相关性检验，如果和之间具有线性相关关系，求出一元线性回归方程；

若某学生入学数学成绩为分，试估计他高一年级期末数学考试成绩．

第7课时

[范例展示]

例1、分析：(1)用平均数公式求解；(2)数值较大，可考虑新数据法

解答：(1)

(2)

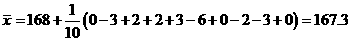
评析：我们在计算平均数时，选择恰当的方法，可以使得计算简单．

例2、分析：(1)将各成绩段人数相加即可；(2)用频数平均数公式计算平均成绩．

解答：(1)共有24名运动员参加比赛．

(2)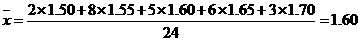(米)．

所以这些运动员的平均成绩为1.60米．

评析：本题也可以用新数据法计算其平均成绩．在用平均数公式解决实际问题时，要灵活选择恰当的平均数计算方法，这样才能使计算简便．

[自我测评]

11．某校高三学生甲、乙两人在月份-月份进行的次模拟考试中，成绩如下：(单位：分)

甲：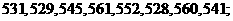

乙：

绘出甲、乙两名学生模拟考试成绩折线图，说明甲、乙两名学生谁的潜力大．

10．已知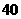个数据的分组以及各组的频数如下：

1－3、2　 9－11、9　 3－5、3　 11－13、5　 5－7、6　 13－15、3　 7－9、10　 15－17、2

列出这组数据的频率分布表，并画出频率分布直方图．　

9．为制定本市初中七、八、九年级学生校服的生产计划，有关部门准备对名初中男生的身高作调查，现有三种调查方案：

．测量少体校中名男子篮球、排球队员的身高；

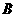．查阅有关外地名男生身高的统计资料；

．在本市的市区和郊县各任选一所完全中学、两所初级中学，在这六所学校有关的年级(1)班中，用抽签的方法分别选出名男生，然后测量他们身高．

为了达到估计本市初中这三个年级男生身高分布的目的，你认为采用上述哪一种调查方案比较合理，为什么？

8．某超市“五一”过后统计了最近6个月某种鲜牛奶的进价和售价(单位：元)的对应数据，如下表：

	3	5	2	8	9	12
	4	6	3	9	12	14

则回归直线方程为　　　　　　　　　　　　　　　 ．

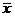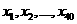7．是的平均数，是的平均数，是的平均数，则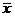，，的之间关系是__________．