
题目列表(包括答案和解析)
5. 椭圆的两焦点把两准线间的距离三等分,则这个椭圆的离心率是 ( )
A 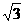 B
B 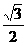 C
C 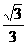 D 以上都不对
D 以上都不对
4.设点P是椭圆 上异于顶点的任意点,作
上异于顶点的任意点,作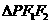 的旁切圆,与x轴的切点为D,则点D ( )
的旁切圆,与x轴的切点为D,则点D ( )
A.在椭圆内 B.在椭圆外 C.在椭圆上 D.以上都有可能
3.椭圆 ,过右焦点F作弦AB,则以AB为直径的圆与椭圆右准线
,过右焦点F作弦AB,则以AB为直径的圆与椭圆右准线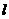 的位置关系是( )
的位置关系是( )
A.相交 B.相离 C.相切 D.不确定
2.曲线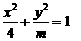 的离心率
的离心率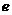 满足方程
满足方程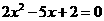 ,则
,则 的所有可能值的积为( )
的所有可能值的积为( )
A.36 B.-36 C.-192 D.-198
1.在椭圆 上取三点,其横坐标满足
上取三点,其横坐标满足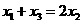 ,三点与某一焦点的连线段长分别为
,三点与某一焦点的连线段长分别为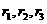 ,则
,则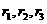 满足( )
满足( )
A.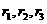 成等差数列 B.
成等差数列 B. 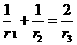 C.
C.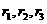 成等比数列 D.以上结论全不对
成等比数列 D.以上结论全不对
23. 在面积为1的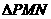 中,
中,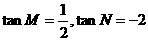 ,建立当的坐标系,求出以M、N为焦点且过点P的椭圆方程.
,建立当的坐标系,求出以M、N为焦点且过点P的椭圆方程.
(目标::能够用解析法求P点坐标,进而求出a,b,c)
[解析]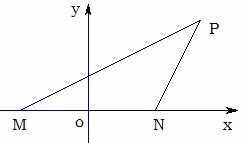 以MN所在的直线为x轴,线段MN的垂直平分线为y轴建立直角坐标系如图:
以MN所在的直线为x轴,线段MN的垂直平分线为y轴建立直角坐标系如图:
设所求方程为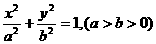 ,则M(-c,0), N(c,0),
,则M(-c,0), N(c,0),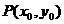
则 
解之得 P(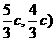
 即
即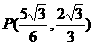

椭圆问题专题讲座
主讲人:郭慧清
地点:D204 时间:2008年12月11日16:45-17:30
22.求中心在原点,一个焦点为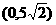 且被直线
且被直线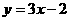 截得的弦中点横坐标为
截得的弦中点横坐标为 的椭圆方程.
的椭圆方程.
(目标:能够用设而不解的方法解决中点弦问题)
[解析] 设椭圆方程  ,弦AB, 中点
,弦AB, 中点 ,
, ,
,
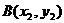 ,则
,则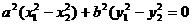 ,
,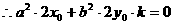
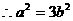 ,又
,又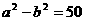 ,
, 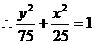 .
.
21.已知曲线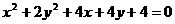 按向量
按向量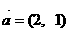 平移后得到曲线C.
平移后得到曲线C.
(1)求曲线C的方程;
(2)过点D(0, 2)的直线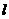 与曲线C相交于不同的两点M、N,且M在D、N之间,设
与曲线C相交于不同的两点M、N,且M在D、N之间,设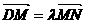 ,求实数
,求实数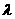 的取值范围.
的取值范围.
解:(1) 由已知设点P(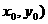 满足
满足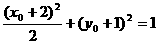 ,点P的对应点Q(
,点P的对应点Q(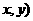
则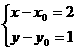
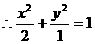 .
.
(2)当直线的斜率不存在时,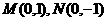 ,此时
,此时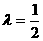 ;
;
当直线的斜率存在时,设l: 代入椭圆方程得:
代入椭圆方程得: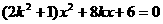
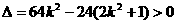 得
得
设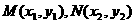 ,则
,则
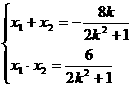 ,
, 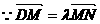
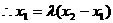 又
又 则
则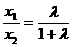 .
.
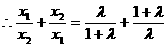 .
.
又
由 ,得
,得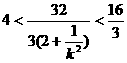 ,即
,即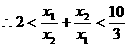
即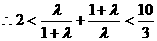 ,又
,又
综上: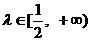
20.已知椭圆的焦点是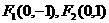 ,直线
,直线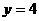 是椭圆的一条准线.
是椭圆的一条准线.
① 求椭圆的方程;
② 设点P在椭圆上,且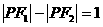 ,求
,求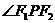 .
.
简解:①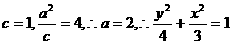 .
.
②设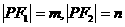 则
则

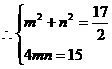
又 
 ,
, 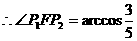
19.如果 满足
满足 则
则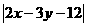 的最大值为
的最大值为 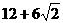
[解析]: 三角代换.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com