
题目列表(包括答案和解析)
1、指数函数的概念(y=ax为什么要规定a>0且a≠1)
2、关系式是否为函数关系?图象如何?
1、找出问题2中的y与x的函数关系.
2、一根一米长的绳子,第一次剪掉绳长的一半,第二次剪掉剩下绳子的一半……,剪了x次后剩余绳子的长度为y米,试写出y与x的函数关系。
1、课本P49,引例
(三)数列中的函数与数形结合思想:
数列是一种特殊的函数,数列的通项公式和前 项和公式都可以看成
项和公式都可以看成 的函数,特别是等差数列的通项公式可以看成是
的函数,特别是等差数列的通项公式可以看成是 的一次函数,而其求和公式可以看成是常数项为零的二次函数,因此许多数列问题可以用函数的思想进行分析,加以解决。
的一次函数,而其求和公式可以看成是常数项为零的二次函数,因此许多数列问题可以用函数的思想进行分析,加以解决。
例3.已知数列 是等差数列,数列
是等差数列,数列 是等比数列,其公比
是等比数列,其公比 ,且
,且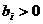 (
(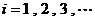 ),若
),若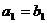 ,
, ,则( )
,则( )
A. 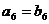 B.
B. 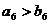 C.
C.  D.
D. 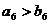 或
或
提示1:等差数列 中的项
中的项 ,等比数列
,等比数列 中的项
中的项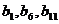 ,你有什么想法?
,你有什么想法?
提示2:数列的本质就是函数,能否从函数的角度解决这个问题呢?
(二)数列中的化归与转化思想:
我们在处理数学问题时,常常将待解决的问题通过转化,化归成为一类我们比较熟悉问题来解决,在数列中常用的就是将非等差、等比问题转化为等差或等比问题来求解。
例2.已知数列 满足
满足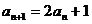 ,且
,且 ,
,
(1)证明数列 是等比数列; (2)求数列
是等比数列; (2)求数列 的通项公式.
的通项公式.
提示1:证明一个数列等比我们最常用什么方法?
提示2:数列 既非等差又非等比,我们可以进行怎样的转化,才可以求其通项?
既非等差又非等比,我们可以进行怎样的转化,才可以求其通项?
(一)数列中的方程思想:
等差数列有两个基本量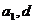 ,等比数列有两个基本量
,等比数列有两个基本量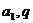 ,等差与等比数列的两个基本问题
,等差与等比数列的两个基本问题 都可以用两个基本量来表示,所以列出关于两个关于基本量的方程组来求解,这种方法又可称为基本量法。
都可以用两个基本量来表示,所以列出关于两个关于基本量的方程组来求解,这种方法又可称为基本量法。
例1. 在等比数列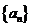 中,如果
中,如果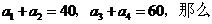
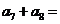 ( )
( )
A.135 B.100 C.95 D.80
运用等比数列的性质怎样求解?(写出解题思路)
常规解法:(写出解题过程)
3、情感态度与价值观:
在运用数学思想方法解决数列问题的过程中培养学生探究学习的习惯并激发其对数学学习的兴趣。
2、过程与方法:
使学生在已掌握的数列题型求解方法上进一步提高解题水平,明确数列与数学思想的内在联系。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com