2.函数y＝x²+2x－3与x 轴两交点之间的距离为______。

1.函数y＝－x²+4x+6 在 上的最大值为_____，最小值为______

3.m为 何值时，抛物线的顶点在x轴下方(　 )

A.m=5　 B.m=－1　　 C.m=5,或m=－1　　 D.m=－5

2.函数y＝x²+4x+a与x轴的两个交点分别位于y轴的两侧则a的取值为______

1．函数y＝－x²+4x+2在0≤x≤3上的最大值为　　 ，最小值为 　　．

(二)二次函数与一元二次方程

1.先来观察几个具体的一元二次方程及其相应的二次函数：

(1)方程与函数

(2)方程与函数

(3)方程与函数

2.问题：一元二次方程的根与二次函数图象和x轴交点坐标有什么关系 ？

3.探究：二次函数图象与一元二次方程根的关系

4.一元二次方程(＞0)根的个数及其判别式与二次函数(＞0)图象与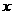轴的位置之间有什么联系？

以＞0为例,如下表所示：

	△﹥0	△=0	△﹤0
(＞0)
(＞0)

[例3]已知二次函数y=x²+ax+a-2

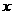(1)求证：不论为任何实数，函数的图象与轴都有两个交点；

(2)试求：当a为何值时，函数图象与x轴的两个交点之间的距离等于；

(3)函数图象与x轴的两个交点分别位于 x=0的两侧，a的取值如何？

[提升训练]

已知二次函数y=x²-(m+2)x+4

(1)求证：不论m为任何实数，函数的图象与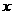轴都有两个交点；

(2)试求：当m为何值时，函数图象与x轴的两个交点之间的距离等于3；

(3)函数图象与x轴的两个交点分别位于x=1的两侧，m的取值如何？

(一)二次函数图像的简单应用--求给定x范围的函数最值

[例1]已知函数y＝x²+2x－3，当自变量x在下列取值范围内时，分别求函数的最大值或最小值，并求当函数取最大(小)值时所对应的自变量x的值：

(1)x≤－2；　　　　　 (2)x≤2；　　　　　　　 (3)－3≤x≤－1；

[练习]

上述函数在下列取值范围内分别求函数的最大值或最小值，并求当函数取最大(小)值时所对应的自变量x的值

(1)x0；　 　　　(2)－3≤x≤0；　　　 (3)-3≤x≤1；　　 (4)-3≤x≤2

[例2]已知函数y＝x²+2x－3，－3≤x≤a，其中a>－3，求该函数的最大值与最小值，并求出函数取最大值和最小值时所对应的自变量x的值．

[变式训练]

已知函数y＝x²－2x+1,－2≤x≤a，其中a>－2，求该函数的最大值与最小值，并求出函数取最大值和最小值时所对应的自变量x的值．

(1)已知与二次函数的图像开口大小相同，开口方向也相同，且图像的顶点为(3,2)，则函数的表达式为________________;

(2)y＝x²+2x－3 的图象的开口向_______;对称轴为_________;顶点坐标为_________;当x＝_________，函数取最______值y＝_____；当x　　　　 时，y随着x的增大而减小．当x-2时，y的取值如何？

4.1二次函数的图像和性质(二)

4.求y=2x²-4x+3当-1x2时的最值