圆的标准方程：以点为圆心，为半径的圆的标准方程是　　　　　　　　　　　 .

特例：圆心在坐标原点，半径为的圆的方程是：　　　　　　　　 .

特殊圆的方程：

①与X轴相切的圆　　　　　　　　　　　　　　 　　　　　

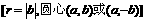
②与Y轴相切的圆　　　　　　　　　　　　　 　　　　　

③与轴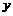轴都相切的圆方程　　　　　　　　　　　　　 　　　

3. 圆的一般方程：　　　　　　　　　　　　　　　　 　.

当　　　　　　　　 时，方程表示一个圆，其中圆心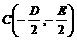，半径.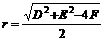

当　　　　　　　　 时，方程表示一个点.

当　　　　　　　　 时，方程无图形.

2.解：点A为y=0与x－2y+1=0两直线的交点，

∴点A的坐标为(－1，0).

∴k_AB=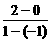=1.

又∵∠A的平分线所在直线的方程是y=0，

∴k _AC=－1.

∴直线AC的方程是y=－x－1.

而BC与x－2y+1=0垂直，∴k_BC=－2.

∴直线BC的方程是y－2=－2(x－1).

y=－2x+4，

解得C(5，－6).

　　　　　　　　　　　　　　　　　 　圆的方程

1.剖析：依据两直线位置关系判断方法便可解决.

解：当m=0时，l₁：x+6＝0，l₂：x＝0，

∴l₁∥l₂.

当m=2时，l₁：x+4y+6＝0，l₂：3y+2＝0，

∴l₁与l₂相交.

当m≠0且m≠2时，由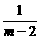＝得m=－1或m=3，由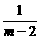＝得m＝3.

故(1)当m≠－1，m≠3且m≠0时，l₁与l₂相交；

(2)当m＝－1或m＝0时，l₁∥l₂；

(3)当m＝3时，l₁与l₂重合.

3.(1)若直线l的斜率存在，设为k，由题意，tan45°=|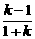|，得k=0，所求l的直线方程为y=－2.

(2)若直线l的斜率不存在，则直线l的方程为x=5，且与直线x－y+5=0相交成45°角.

综合(1)(2)，直线l的方程为x=5或y=－2.

解答题：

2.解析：利用两直线平行的条件.

答案：－1

1.解析：y=|x|是第一、二象限角的平分线，直线y=kx+1是过定点(0，1)的直线系方程.

由图象易知－1<k<1.

答案：－1<k<1

2.在△ABC中，已知BC边上的高所在直线的方程为x－2y+1=0，∠A的平分线所在直线的方程为y=0.若点B的坐标为(1，2)，求点C的坐标.

答案详解：

基础训练：

k₁=k₂且b₁≠b₂.；k₁·k₂=－1；平行或重合；l₁⊥l₂ 有唯一解；无解；有无数解；；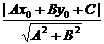

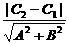
选择：B，B，A，B，B，A

填空题：

1.已知两直线l₁：x+m²y+6＝0，l₂：(m－2)x+3my+2m＝0，当m为何值时，l₁与l₂(1)相交；(2)平行；(3)重合?

3.过点P(5，－2)，且与直线x－y+5=0相交成45°角的直线l的方程为　　　　　　　　

2.若直线l₁：ax+2y+6=0与直线l₂：x+(a－1)y+(a²－1)=0平行且不重合，则a的值是____________.