
题目列表(包括答案和解析)
2. 函数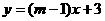 在R上是增函数,则m的取值范围是( )
在R上是增函数,则m的取值范围是( )
A.  B.
B.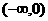 C.
C. D.
D.
1. 下列四个函数中,在(0,+ )上增函数的是 ( )
)上增函数的是 ( )
A.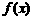 =
= B.
B. C.
C.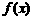 =
= D.
D.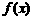 =-|x|
=-|x|
2. 证明:如图,连结OP、BP.
证明:如图,连结OP、BP.
∵AB是⊙O的直径,∴∠APB=90°.
又∵CE=BE,∴EP=EB. ∴∠3=∠1.
∵OP=OB,∴∠4=∠2.
∵BC切⊙O于点B,∴∠1+∠2=90°.
∠3+∠4=90°.
又∵OP为⊙O的半径,
∴PE是⊙O的切线.
综合练习(一)
1. 解:如右图,延长AP交⊙O于点D.
解:如右图,延长AP交⊙O于点D.
由相交弦定理,知 .
.
∵PA=2cm,PB=5cm,PC=3cm,
∴2PD=5×3. ∴PD=7.5.
∴AD=PD+PA=7.5+2=9.5.
∵MN切⊙O于点A,AP⊥MN,
∴AD是⊙O的直径.
∴⊙O的直径是9.5cm.
2.如图,AB为⊙O的直径,BC切⊙O于B,AC交⊙O于P,CE=BE,E在BC上. 求证:PE是⊙O的切线.

答案详解:
基础知识: ;
;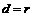 ;公切弦方程.;
;公切弦方程.; ;
; ;
; ;
; ;
; ;
;
选择题:C;A;D;A;C;B;
填空题:1. 15°; 2. 5; 3. 40
解答题:
1.如图,MN为⊙O的切线,A为切点,过点A作AP⊥MN,交⊙O的弦BC于点P. 若PA=2cm,PB=5cm,PC=3cm,求⊙O的直径.

3.AD、AE和BC分别切⊙O于D、E、F,如果AD=20,则△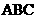 的周长为
的周长为

2. 如图,已知⊙O的直径AB与弦AC的夹角为30°,过C点的切线PC与AB的延长线交于P,PC=5,则⊙O的半径为
如图,已知⊙O的直径AB与弦AC的夹角为30°,过C点的切线PC与AB的延长线交于P,PC=5,则⊙O的半径为
1.A、B、C是⊙O上三点,的度数是50°,∠OBC=40°,则∠OAC等于
6.把直线 绕原点逆时针方向旋转,使它与圆
绕原点逆时针方向旋转,使它与圆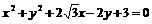 相切,则直线转动的最小正角是( )
相切,则直线转动的最小正角是( )
A. B.
B.  C.
C. D.
D.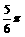
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com