1．某种电热水器的水箱盛满水时200升，加热到一定温度即可浴用，浴用前，已知每分钟放水34升，在放水的同时按毫升／秒²的匀加速自动注水(即分钟自动注水升)当水箱内的水达到最小值时，放水过程自动停止．现假定每人洗浴用量为65升，则该热水器一次至多可供多少人洗浴(　)

A．3　B．4　C．5　D．6

4． f(x)=a+bx+c(a0)当a>0时,增区间为　　　　　 ；减区间为　　　　　　　 ．

[典例解析]

例1．《民共和国个人所得税法》十四条中有表：

个人所得税税率表(工资 / 薪金所得使用)

目前,上表中＂全月应纳税所得额＂是从工资 薪金收入中减去800元后的余额．如，某人月工资薪金收入1320元，减去800元，应纳税所得额为520元，由税率表知其中500元税率为5%，另20元的税率为10%，所以此人应纳个人所得税500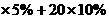＝27元．

(1)　 请写出月工资薪金的个人所得税y关于工资薪金收入x(0＜x10000)的函数表达式；

(2)　 某人在某月交纳的个人所得税是120元，他那个月的工资薪金收入是多少？

例2：渔场中鱼群的最大养殖量是m吨，为保证鱼群的生长空间，实际养殖量不能达到最大养殖量，必须留出适当的空闲量。已知鱼群的年增长量y吨和实际养殖量x吨与空闲率乘积成正比，比例系数为k(k＞0)．

(1)　 写出y关于x的函数关系式，指出这个函数的定义域；

(2)　 求鱼群年增长量的最大值；

(3)　 当鱼群的年增长量达到最大值时，求k的取值范围．

例3：某摩托车生产企业，上年度生产摩托车的投入成本为1万元／辆，出厂价为1．2万元／辆，年销量为1000。为适应市场需求，计划提高产品档次，适度增加投入成本，若每辆车投入成本增加的比例为x(0＜x＜1＝，则出厂价相应的提高比例为0．75x，同时预计年销售量增加的比例为0.6，利润＝(出厂价－投入成本)年销售量。

(1)　 写出本年度预计的年利润y与投入成本增加的比例x的关系式；

(2)　 为使本年度的年利润比上年有说增加，问投入成本增加的比例x应在什么范围？

[当堂练习]

3．f(x)=a+bx+c(a0)，当a　 0,其图象开口向　　 ，函数有最　 值,为　　　　 ；

当a　 0, 其图象开口向　　 ，函数有最　 值,为　　　　 。(当给定一区间的二次函数的最值问题怎样考虑？)

2．二次函数的解析式三种常见形式为　　　　　　　　　　 ；

　　　　　　　　 ；　　　　　　　　　　 。

1．形如f(x)=　　　　　　 叫一次函数，当　　　　 为增函数；当为减函数。

2.3 函数的应用(一)学案

[预习达标]

5．例题思考：

例1：例1：求下列函数的定义域(用区间表示)

　 f(x)=；　 f(x)=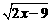； f(x)=－

例2：用两种方法求下列函数的定义域与值域：y=； ；　 y=2x+1　　 y=ax+1　 (a＞0)

思考(如果在给定区间x∈[1，2]上，函数的值域如何求

4．知识点小结：

3．思考并回答以下问题：

(1)区间与集合的联系是什么？

(2)闭区间与开区间的区别是什么？

(3)你能总结几个简单函数的定义域和值域吗？

(4)如何判断两个函数相同？

2．自学内容：通读教材17页3行至18页，约用10分钟。