
题目列表(包括答案和解析)
9.已知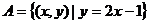 ,
,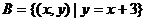 ,
, ,
, ,求
,求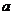 。
。
8.集合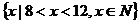 ,用列举法可表示为_____________。
,用列举法可表示为_____________。
7.设直线 上的点集为P,则P=____________。点(2,7)与P的关系为(2,7)___________P。
上的点集为P,则P=____________。点(2,7)与P的关系为(2,7)___________P。
6.1_________ 。
。
5.0_______
4、(1)已知集合 ,则M=
,则M=
(2)已知集合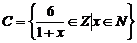 ,则C=
,则C=
3.已知 ,定义
,定义 ,则集合
,则集合 等于( )
等于( )
A. B.
B. C.
C. D.
D.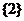
2.已知集合S={ }中的三个元素可构成
}中的三个元素可构成 ABC的三条边长,那么
ABC的三条边长,那么 ABC一定不是( )
ABC一定不是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
1.下面四个命题正确的是( )
A.10以内的质数集合是{0,3,5,7}
B.“个子较高的人”不能构成集合
C.方程 的解集是{1,1}
的解集是{1,1}
D.偶数集为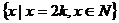
[考题1]已知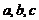 为非零实数,用列举法写出
为非零实数,用列举法写出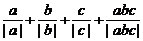 的所有值组成的集合。
的所有值组成的集合。
[解析]当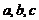 都是正数时,
都是正数时, ;
;
当 中有且仅有两个是正数时,
中有且仅有两个是正数时,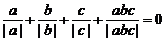 ;
;
当 中有且仅有一个是正数时,
中有且仅有一个是正数时,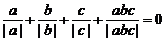 ;
;
当 都是负数时,
都是负数时,
因为集合中的元素都是互异的,所以所求集合为
[点评]在用列举法写数集时,注意格式: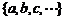 ,即把集合中所有的元素(数值)一一列举出来,并用逗号隔开,放到花括号内即可。
,即把集合中所有的元素(数值)一一列举出来,并用逗号隔开,放到花括号内即可。
[考题2]用符号 或
或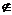 填空:
填空:
(1)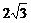
 ;
;
(2)3  ;
;
(3)
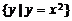 ,
,
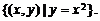
[解析](1)∵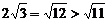 ,∴
,∴
(2)令 ,则
,则 ,
,
∴
(3)∵ 是一个有序实数时,且符号关系
是一个有序实数时,且符号关系 ,
,
∴ ,
,
[点评]对于(3),要注意描述法中的符号“ ”左边元素的形式,
”左边元素的形式,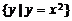 表示函数
表示函数 的函数值的集合,
的函数值的集合, 表示满足
表示满足 的图象上的点集,其中一个是“数”为元素,另一个是以“点”或“实数对”为元素,两个集合是不同的集合。
的图象上的点集,其中一个是“数”为元素,另一个是以“点”或“实数对”为元素,两个集合是不同的集合。
[考题3]用列举法表示下列集合:
(1)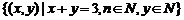 ;
;
(2)
[解析]集合中的元素是有序数对 ,可以理解为直角坐标系上点的坐标,因此,此题给的集合可以理解为点集。
,可以理解为直角坐标系上点的坐标,因此,此题给的集合可以理解为点集。
(1) 都是自然数,而
都是自然数,而 故集合为
故集合为
(2)∵ ,∴
,∴ ,相应的
,相应的 故集合为
故集合为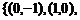

[点评]若 ,则
,则 与
与 表示不同的元素。
表示不同的元素。
[考题4]可以表示方程组 的解集是 。(写出所有正确答案的序号)
的解集是 。(写出所有正确答案的序号)
(1) ; (2)
; (2)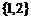 ;(3)
;(3) ;(4)
;(4) ;
;
(5)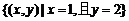 ;(6)
;(6) ;(7)
;(7)
[解析]方程组的解 是一组数对
是一组数对 ,所以解集可用列举法表示为
,所以解集可用列举法表示为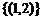 ,也可用特征性质描述法表示为
,也可用特征性质描述法表示为 又(5),(6),(7)和(3)等价。
又(5),(6),(7)和(3)等价。
[点评](1)中存在两个元素,它表示两个方程;(2)中是两个元素,表示的是两个数,这些都不能表示原方程组的解集。
容易出错且难于理解的是(4),由于集合的代表元素也是数对 ,因而该集合表示直角坐标平面上的点集,问题是:
,因而该集合表示直角坐标平面上的点集,问题是: 和
和 之间用“或”连接,说明它们之间是并列关系,所以该集合表示直线
之间用“或”连接,说明它们之间是并列关系,所以该集合表示直线 与直线
与直线 上的所有点的集合。
上的所有点的集合。
[考题5]设集合 ,且
,且 ,求实数
,求实数
[解析]解法一:∵ ,∴
,∴ 中元素分别对应相同。
中元素分别对应相同。
∴ 即
即
∵集合中元素互异,∴ 于是可求得
于是可求得
解法二:∵ ,∴
,∴
∵集合的元素经异,∴ 。于是可得
。于是可得
[考题6]已知集合 ,若
,若 求
求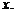
[解析]当 时,
时, ,
, 或
或
经检验, 均不合题意。
均不合题意。
当 时,
时, 或2。
或2。
经检验,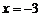 或
或 均合题意。
均合题意。
∴ 或
或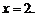
[点评]要把所得的解代入原集合,验证元素的互异性,因为集合M用列举法给出就隐含了M中的三个元素互不相等。
[考题7]下列命题:
(1)方程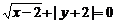 的解集为
的解集为 ;
;
(2)集合 与
与 的公共元素所组成的集合是
的公共元素所组成的集合是 ;
;
(3)集合 与集合
与集合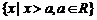 没有公共元素。
没有公共元素。
其中真命题的个数有( )
A.0 B.1 C.2 D.3
[解析]要判断这些命题的真假,就需要对用来描述这些命题的集合语言进行转化,以弄清集合的构成。在(1)中方程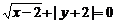 等价于
等价于 即
即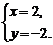 其解
其解
 应为有序实数对,因此其解集应为
应为有序实数对,因此其解集应为 ,故命题(1)是假命题。而在(2)中,由于集合
,故命题(1)是假命题。而在(2)中,由于集合 的代表元素是
的代表元素是 ,而
,而 满足属性:“
满足属性:“ ”。由于当
”。由于当 时,
时,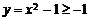 ,所以集合
,所以集合 是由大于或等于
是由大于或等于 的实数所组成的集合。同理
的实数所组成的集合。同理 ,因此(2)也是错误的。在(3)中,集合
,因此(2)也是错误的。在(3)中,集合 即为不等式
即为不等式 的解集,而
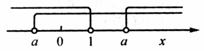
的解集,而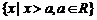 为不等式
为不等式 的解集。由图可知,这两个集合可能有公共的元素,也可能没有公共的元素,因此(3)也是错误的。故选A。
的解集。由图可知,这两个集合可能有公共的元素,也可能没有公共的元素,因此(3)也是错误的。故选A。
[点评]在(2)中,很容易被符号描述法的表象所蒙蔽,认为这两个集合中的“ ”和“
”和“ ”必须取相同的值。事实上,这是用相同字母来描述不同的集合的元素所具有的属性。
”必须取相同的值。事实上,这是用相同字母来描述不同的集合的元素所具有的属性。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com