
题目列表(包括答案和解析)
4.有下列四个命题:
(1)“若xy = 1, 则x,y互为倒数”的逆命题
(2)“面积相等的三角形全等”的否命题
(3)“若m 1, 则
1, 则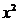 -2x+m=0有实数解”的逆否命题
-2x+m=0有实数解”的逆否命题
(4)“若A B = B, 则A
B = B, 则A ” 的逆否命题
” 的逆否命题
其中真命题为 ( )
A.⑴⑵ B.⑵⑶ C.⑶⑷ D.⑴⑵⑶
3.下列各组命题中,满足“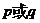 ”为真,“
”为真,“ ”为假,“非p”为真的是 ( )
”为假,“非p”为真的是 ( )
A. 
B.  则A=B, q: 在第一象限是增函数
则A=B, q: 在第一象限是增函数
C. 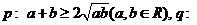 不等式
不等式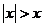 的解集为
的解集为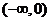
D. p: 圆 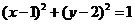 的面积被直线x=1平分, q: 椭圆
的面积被直线x=1平分, q: 椭圆 的一条
的一条
准线方程是x=4.
2.(2005•浙江)设 为两个不同的平面,
为两个不同的平面, 为两条不同的直线,且
为两条不同的直线,且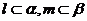 ,
,
有如下的两个命题:①若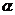 ∥
∥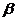 ,则l∥m;②若l⊥m,则
,则l∥m;②若l⊥m,则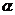 ⊥
⊥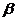 .那么 ( )
.那么 ( )
A.①是真命题,②是假命题 B. ①是假命题,②是真命题
C.①②都是真命题 D. ①②都是假命题
1.(2005•广东)给出下列关于互不相同的直线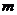 、
、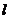 、
、 和平面
和平面 、
、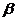 ,的四个命题:
,的四个命题:
①若 ,点
,点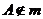 ,则
,则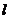 与
与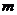 不共面;
不共面;
②若m、l是异面直线, 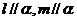 , 且
, 且 ,则
,则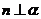 ;
;
③若 ,
,  ,则
,则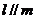 ;
;
④若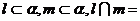 点
点 ,
, ,则
,则 .
.
其中为假命题的是( )
A.① B.② C.③ D.④
2.想不到用判断逆否命题的真假的方法来判断原命题的真假.
[基础演练]
1.混淆命题的否定与命题的否命题的区别而出错.否命题与命题的否定是完全不同的两个概念,如:已知命题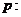 “若
“若 ,则方程
,则方程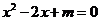 无实数根”,其非
无实数根”,其非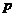 形式为“若
形式为“若 ,则方程
,则方程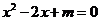 有实数根”;
有实数根”; 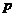 的否命题为:“若
的否命题为:“若 ,则方程
,则方程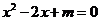 有实数根”.
有实数根”.
1.对命题真假的判断或考查一命题的否定与非命题如例1,例2,例3 .
[典例精析]
例1(2005•天津)给出下列三个命题
① 若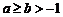 ,则
,则 ;
;
② 若正整数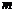 和
和 满足
满足 ,则
,则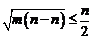 ;
;
③ 设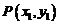 是圆
是圆 上的任意一点,圆
上的任意一点,圆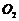 以
以 为圆心,且半径为1。当
为圆心,且半径为1。当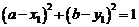 时,圆
时,圆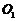 与
与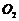 圆相切.
圆相切.
其中假命题的个数为( )
A.0 B.1 C.2 D.3
解析:① 用“分部分式”判断,具体:
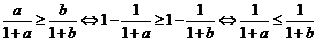 ,又
,又 知本命题为真命题.
知本命题为真命题.
② 用基本不等式: (
(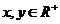 ),取
),取 ,
, ,知本命题为真.
,知本命题为真.
③ 圆 上存在两个点A、B满足正弦
上存在两个点A、B满足正弦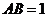 ,所以P、
,所以P、 可能都在圆
可能都在圆 上,当
上,当 在圆
在圆 上时,圆
上时,圆 圆
圆 相交。故本命题假命题.
相交。故本命题假命题.
答案:B.
例2(2005•江苏)设 为两两不重合的平面,l,m,n为两两不重合的直线,给出下列四个命题:
为两两不重合的平面,l,m,n为两两不重合的直线,给出下列四个命题:
①若 则
则 ∥
∥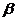 ;
;
②若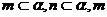 ∥
∥ ∥
∥ 则
则 ∥
∥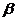 ;
;
③若 ∥
∥ 则
则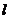 ∥
∥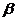 ;
;
④若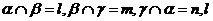 ∥
∥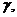 则m∥n.
则m∥n.
其中真命题的个数是( )
A.1 B.2 C.3 D.4
解析:①由面面垂直知,不正确;
②由线面平行判定定理知,缺少m、n相交于一点这一条件,故不正确;
③由线面平行判定定理知,正确;
④由线面相交、及线面、线线平行分析知,正确.
综上所述知,③,④正确.
答案:B.
例3.(2004•北京春)已知三个不等式:
 (其中
(其中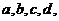 均为实数).用其中两个不等式作为条件,余下的一个不等式结论组成一个命题,可组成正确的命题的个数是( )
均为实数).用其中两个不等式作为条件,余下的一个不等式结论组成一个命题,可组成正确的命题的个数是( )
A.0 B.1 C.2 D.3.
解析:易知由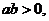
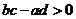

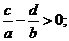
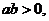
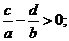

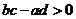
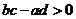


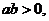 可组成正确命题个数是3个.
可组成正确命题个数是3个.
答案:D.
[常见误区]
2.理解四种命题及其相互关系.
1.理解逻辑联结词“或”、“且”、“非”的含义.
1.2命题
[考点透视]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com