
题目列表(包括答案和解析)
3.在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立
的是 ( )
A.BC//平面PDF B.DF⊥PAE
C.平面PDF⊥平面ABC D.平面PAE⊥平面ABC
2.已知 是定义在R上的单调函数,实数
是定义在R上的单调函数,实数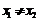 ,
,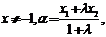
 ,
,
若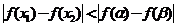 则 ( )
则 ( )
A.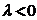 B.
B.  C.
C. 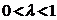 D.
D. 
1.用反证法证明:“若m Z且m为奇数,则
Z且m为奇数,则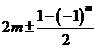 均为奇数”,其假设正确的是
均为奇数”,其假设正确的是
( )
A.都是偶数 B.都不是奇数 C.不都是奇数 D.都不是偶数
2.不知道要推出怎样的矛盾,其实可能出现以下四种情况:①导出非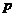 为真及与原命题的条件矛盾:②导出
为真及与原命题的条件矛盾:②导出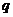 为真,即与假设非
为真,即与假设非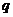 为真矛盾;③导出一个恒假命题:④一出自相矛盾.
为真矛盾;③导出一个恒假命题:④一出自相矛盾.
[基础演练]
1.用反证法证明若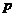 则
则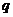 时,不能正确的写出假设,从而导致错误;
时,不能正确的写出假设,从而导致错误;
2.在判断线与线,线与面,面与面的平行、垂直等关系时常用反证法思想方法.
[典例精析]
例1.对于函数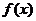 ,若存在
,若存在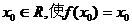 成立,则称
成立,则称 的不动点。如果函数
的不动点。如果函数 有且只有两个不动点0,2,且
有且只有两个不动点0,2,且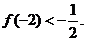
(1)求函数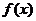 的解析式;
的解析式;
(2)已知各项不为零的数列 ,求数列通项
,求数列通项 ;
;
(3)如果数列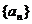 满足
满足 ,求证:当
,求证:当 时,恒有
时,恒有 成立.
成立.
解析: (1) 依题意有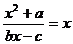 ,化简为
,化简为  由韦达定理, 得
由韦达定理, 得
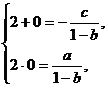
解得 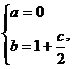 代入表达式
代入表达式 ,由
,由
得 
 不止有两个不动点,
不止有两个不动点,
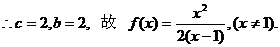
(2)由题设得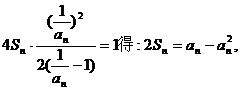 (*)
(*)
且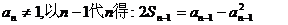 (**)
(**)
由(*)与(**)两式相减得:
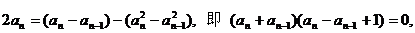

解得 (舍去)或
(舍去)或 ,由
,由 ,若
,若 这与
这与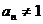 矛盾,
矛盾, ,即{
,即{ 是以-1为首项,-1为公差的等差数列,
是以-1为首项,-1为公差的等差数列, .
.
(3)采用反证法,假设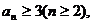 则由(1)知
则由(1)知 ,
,
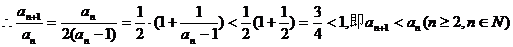 ,有
,有
 ,而当
,而当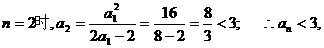 这与假设矛盾,故假设不成立,
这与假设矛盾,故假设不成立, .
.
例2:(2005•北京)设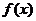 是定义在[0,1]上的函数,若存在
是定义在[0,1]上的函数,若存在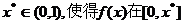 上单调递增,在[x*,1]上单调递减,则称
上单调递增,在[x*,1]上单调递减,则称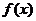 为[0,1]上的单峰函数,x*为峰点,包含峰点的区间为含峰区间.
为[0,1]上的单峰函数,x*为峰点,包含峰点的区间为含峰区间.
对任意的[0,1]上的单峰函数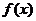 ,下面研究缩短其含峰区间长度的方法.
,下面研究缩短其含峰区间长度的方法.
(1)证明:对任意的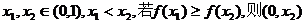 为含峰区间;
为含峰区间;
若 为含峰区间;
为含峰区间;
(2)对给定的r(0<r<0.5),证明:存在 ,使得由(Ⅰ)所确定的含峰区间的长度不大于0.5+r;
,使得由(Ⅰ)所确定的含峰区间的长度不大于0.5+r;
(3)选取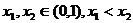 ,由(Ⅰ)可确定含峰区间为(0,
,由(Ⅰ)可确定含峰区间为(0, )或(
)或(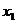 ,1),在所得的含峰区间内选取
,1),在所得的含峰区间内选取 类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0,
类似地可确定一个新的含峰区间,在第一次确定的含峰区间为(0, )的情况下,试确定
)的情况下,试确定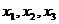 的值,满足两两之差的绝地值不小于0.02,且使得新的含峰区间的长度缩短到0.34.(区间长度等于区间的右端点与左端点之差)
的值,满足两两之差的绝地值不小于0.02,且使得新的含峰区间的长度缩短到0.34.(区间长度等于区间的右端点与左端点之差)
解析:(1)设 为
为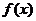 的峰点,则由单峰函数定义可知
的峰点,则由单峰函数定义可知 在
在 上单调递增,
上单调递增,
在 上单调递减.当
上单调递减.当 时,假设
时,假设 ,则
,则 从而
从而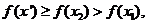 这与
这与 矛盾,所以
矛盾,所以 ,即
,即 是含峰区间.
是含峰区间.
当 时,假设
时,假设 ,则
,则 ,从而
,从而 这与
这与 矛盾,所以
矛盾,所以 ,即
,即 是含峰区间.
是含峰区间.
(2)由(1)的结论可知:当 时,含峰区间的长度为
时,含峰区间的长度为 当
当 时,含峰区间的长度为
时,含峰区间的长度为 对于上述两种情况,由题意得
对于上述两种情况,由题意得
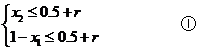
由①得 ,即
,即 又因为
又因为 ,所以
,所以

将②代入①得

由①和③解得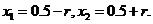
所以这时含峰区间的长度 ,即存在
,即存在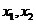 使得所确定的含峰区间
使得所确定的含峰区间
的长度不大于
(3)对先选择的 ,由(II)可知
,由(II)可知
在第一次确定的含峰区间为 的情况下,
的情况下,  的取值应满足
的取值应满足
由④与⑤可得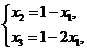 当
当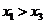 时,含峰区间的长度为
时,含峰区间的长度为 由条件
由条件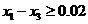 ,得
,得 ,从而
,从而 因此,为了将含峰区间的长度缩短到
因此,为了将含峰区间的长度缩短到 ,只要取
,只要取 
例3:(2005•湖南)已知函数f(x)=lnx,g(x)= ax2+bx,a≠0.
ax2+bx,a≠0.
(1)若b=2,且h(x)=f(x)-g(x)存在单调递减区间,求a的取值范围;
(2)设函数f(x)的图象C1与函数g(x)图象C2交于点P、Q,过线段PQ的中点作x轴的垂线分别交C1,C2于点M、N,证明C1在点M处的切线与C2在点N处的切线不平行.
解析:(1) ,则
,则
因为函数h(x)存在单调递减区间,所以 <0有解.
<0有解.
又因为x>0时,则ax2+2x-1>0有x>0的解.
①当a>0时,y=ax2+2x-1为开口向上的抛物线,ax2+2x-1>0总有x>0的解;
②当a<0时,y=ax2+2x-1为开口向下的抛物线,而ax2+2x-1>0总有x>0的解;
则△=4+4a>0,且方程ax2+2x-1=0至少有一正根.此时,-1<a<0.
综上所述,a的取值范围为(-1,0)∪(0,+∞).
(2)设点P、Q的坐标分别是(x1, y1),(x2, y2),0<x1<x2.
则点M、N的横坐标为 C1在点M处的切线斜率为
C1在点M处的切线斜率为
C2在点N处的切线斜率为
假设C1在点M处的切线与C2在点N处的切线平行,则k1=k2,即 ,于是
,于是
=
所以 设
设 则
则 ①
①
令 则
则
因为 时,
时, ,所以
,所以 在
在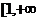 )上单调递增. 故
)上单调递增. 故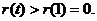
则 . 这与①矛盾,假设不成立.
. 这与①矛盾,假设不成立.
故C1在点M处的切线与C2在点N处的切线不平行.
[常见误区]
1.常与函数、数列、解析几何的综合题结合在一起考查反证法的技巧;
1.会用反证法证明简单的问题.
1.4 反证法
[考点透视]
9.已知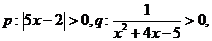 则
则
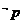 是
是 的什么条件?
的什么条件?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com