
题目列表(包括答案和解析)
3.分类讨论的思想
利用分类讨论的思想解答分类讨论问题已成为高考中考考查学生知识和能力的热点问题。这是因为:其一,分类讨论问题一般都覆盖较多知识点,有利于对学生知识面的考查;其二,解分类讨论问题需要有一定的分析能力,一定的分类讨论思想与技巧,因此有利于对能力的考查;其三,分类讨论问题常与实际问题和高等数学相联系。
解分类讨论问题的实质是:整体问题化为部分来解决,化成部分后,从而增加题设条件,这也是解分类问题总的指导思想。
2.数形结合的思想
数形结合的思想是数学重要的思想方法之一,数形结合的解题方法的特点是:具有直观性、灵活性、深刻性,并跨越各科的界线,有较强的综合性,加强这方面的学习和训练,对巩固数学知识,打好基础、提高能力是重要一环。
[例]对于任意 ,函数
,函数 表示
表示 中的较大者,则
中的较大者,则 的最小值是 。
的最小值是 。
[解析]首先应理解题意,“函数 表示
表示 中的较大者。”是指对某个区间而言,函数
中的较大者。”是指对某个区间而言,函数 表示
表示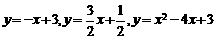 中最大的一个。
中最大的一个。
 如图,分别画出三个函数
如图,分别画出三个函数 的图象,得到三个交点
的图象,得到三个交点 。
。
从图象观察可得函数 表达式。
表达式。
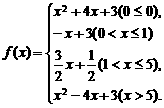
 的图象是图中的实线部分,图象的最低点是点
的图象是图中的实线部分,图象的最低点是点 ,故函数
,故函数 的最小值是2。
的最小值是2。
[点评]本题若不用图象法,单就求出这个分段函数中每一段 的取值范围就很复杂了。
的取值范围就很复杂了。
1.函数的思想
函数的思想方法,既是先构造辅助函数,将所给问题转化为构造的辅助函数的性质(如单调性、奇偶性、最值等)研究后,得出所需的结论。
利用函数思想处理问题,必须深刻理解、熟练掌握一次函数、反比例函数、二次函数的具体特征及一般函数 的单调性、奇偶性、最值、图象变换等,这是利用函数的思想解题的必备基础。
的单调性、奇偶性、最值、图象变换等,这是利用函数的思想解题的必备基础。
同时要善于观察问题的结构特征,提示内在联系,挖掘隐含的特性,从而恰当构造函数和准确地利用函数性质,使问题得以解决。
要注意幂函数、指数函数、对数函数的定义域和值域等性质的研究,尤其是它的复合函数的性质研究。
[例1]设对所有实数 ,不等式
,不等式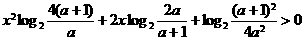 恒成立,求
恒成立,求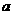 的取值范围。
的取值范围。
[解析]解析一:可利用代换法,将问题转化为一元二次不等式问题处理。
解:令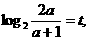
则原不等式变为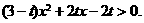 ①
①
当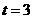 时,①式变为
时,①式变为 ,得
,得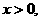
这与题设对所有实数 不等式①恒成立相矛盾。
不等式①恒成立相矛盾。
∴
当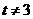 ,即
,即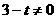 时,使①对所有实数
时,使①对所有实数 恒成立,需
恒成立,需
 得
得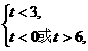 则
则
∴
∴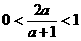 ,解得
,解得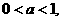
∴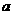 的取值范围为(0,1)为所求。
的取值范围为(0,1)为所求。
解析二:本题是关于 为“主元”的一元二次不等式,常规思路是由“
为“主元”的一元二次不等式,常规思路是由“ ”,列出不等式组进行求解,但形式复杂,运算冗繁,令人望而生畏,往往半途而废,若反客为主,视为关于
”,列出不等式组进行求解,但形式复杂,运算冗繁,令人望而生畏,往往半途而废,若反客为主,视为关于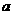 为主元的对数不等式,则是另一番情景。
为主元的对数不等式,则是另一番情景。
解:将原不等式化为
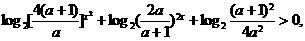
即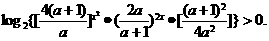
所以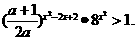
因为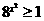 且
且 ,欲使原不等式对
,欲使原不等式对 恒成立,必须
恒成立,必须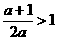 ,解得
,解得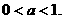
[点评]有些数学问题构思新颖,同时有其实际背景,按固有习惯思维,把注意力集中在某些醒目的“主元”上,往往陷入困境,如果打破思维定势,反“客”为“主”,把原来处于相对次要地位的“客元”找出来,常常能收到出人意料的效果。
[例2]定义在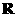 上的函数
上的函数 满足
满足 ,
,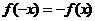 ,当
,当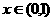 时,
时,
(1)求 在
在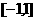 上是解析式;
上是解析式;
(2)证明 在(0,1)上是减函数;
在(0,1)上是减函数;
(3)当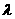 取何值时,方程
取何值时,方程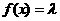 在
在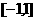 上有解。
上有解。
解析:根据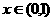 时函数的解析式及条件
时函数的解析式及条件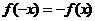 ,可求出
,可求出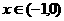 时函数的解析式,根据
时函数的解析式,根据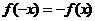 又可求出
又可求出 的值,怎样求
的值,怎样求 、
、 呢?需用条件
呢?需用条件 ,为了研究方程
,为了研究方程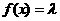 在
在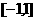 有解,可转化为求函数
有解,可转化为求函数 在
在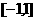 上的值域。
上的值域。
(1)设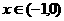 ,则
,则
∵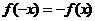 ,且
,且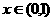 时,
时, ,
,
∴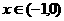 时,有
时,有
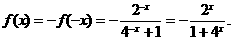
在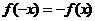 中,
中,
令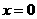 ,得
,得
∵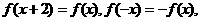
令 ,得
,得
∴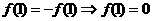 ,从而
,从而
∴当 时有
时有

(2)设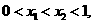
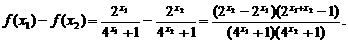
∵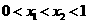 ,∴
,∴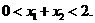 ∴
∴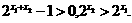
又∵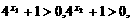
∴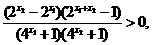
即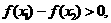 ∴
∴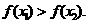
∴ 在(0,1)上是减函数。
在(0,1)上是减函数。
(3)方程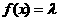 在
在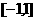 上有解的充要条件是
上有解的充要条件是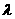 在函数
在函数 的值域内取值。
的值域内取值。
∵ 时,
时,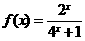 是减函数.
是减函数.
∴ 时,
时,
∵ ,
,
∴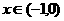 时,
时,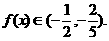
又
∴ 时,函数
时,函数 的值域为
的值域为
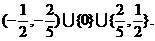
∴当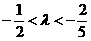 或
或 或
或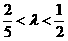 时,方程
时,方程 在
在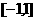 上有解。
上有解。
[点评]在第(1)问中,利用函数的一般性质求解在特殊点的函数值是解题中一种重要方法和技巧,在第(3)问中,应用了“函数方程思想”。
[例3]已知函数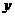 =
= +
+ 有如下性质:如果常数
有如下性质:如果常数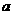 >0,那么该函数在
>0,那么该函数在 0,
0,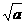
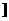 上是减函数,在
上是减函数,在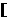
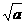 ,+∞
,+∞ 上是增函数.
上是增函数.
(1)如果函数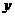 =
= +
+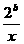 (
( >0)的值域为
>0)的值域为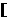 6,+∞
6,+∞ ,求
,求 的值;
的值;
(2)研究函数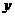 =
=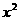 +
+ (常数
(常数 >0)在定义域内的单调性,并说明理由;
>0)在定义域内的单调性,并说明理由;
(3)对函数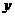 =
= +
+ 和
和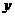 =
=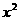 +
+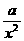 (常数
(常数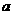 >0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数
>0)作出推广,使它们都是你所推广的函数的特例.研究推广后的函数的单调性(只须写出结论,不必证明),并求函数 =
=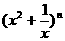 +
+ (
( 是正整数)在区间[
是正整数)在区间[ ,2]上的最大值和最小值(可利用你的研究结论).
,2]上的最大值和最小值(可利用你的研究结论).
解析:(1) 函数y=x+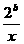 (x>0)的最小值是2
(x>0)的最小值是2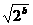 ,则2
,则2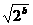 =6, ∴b=log29.
=6, ∴b=log29.
(2)设0<x1<x2,y2-y1=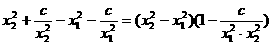 .
.
当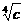 <x1<x2时, y2>y1, 函数y=
<x1<x2时, y2>y1, 函数y=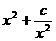 在[
在[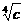 ,+∞)上是增函数;
,+∞)上是增函数;
当0<x1<x2<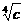 时y2<y1,
函数y=
时y2<y1,
函数y=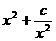 在(0,
在(0,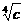 ]上是减函数.
]上是减函数.
又y=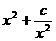 是偶函数,于是,该函数在(-∞,-
是偶函数,于是,该函数在(-∞,-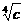 ]上是减函数, 在[-
]上是减函数, 在[-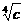 ,0)上是增函数.
,0)上是增函数.
(3)可以把函数推广为y= (常数a>0),其中n是正整数.
(常数a>0),其中n是正整数.
当n是奇数时,函数y= 在(0,
在(0,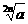 ]上是减函数,在[
]上是减函数,在[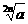 ,+∞) 上是增函数,
,+∞) 上是增函数,
在(-∞,-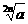 ]上是增函数, 在[-
]上是增函数, 在[-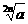 ,0)上是减函数.
,0)上是减函数.
当n是偶数时,函数y= 在(0,
在(0,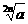 ]上是减函数,在[
]上是减函数,在[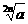 ,+∞) 上是增函数,
,+∞) 上是增函数,
在(-∞,-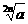 ]上是减函数, 在[-
]上是减函数, 在[-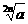 ,0)上是增函数.
,0)上是增函数.
F(x)= 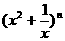 +
+
=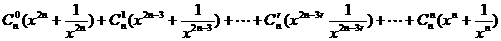
因此F(x) 在 [ ,1]上是减函数,在[1,2]上是增函数.
,1]上是减函数,在[1,2]上是增函数.
所以,当x= 或x=2时, F(x)取得最大值(
或x=2时, F(x)取得最大值( )n+(
)n+( )n;
)n;
当x=1时F(x)取得最小值2n+1.
3、三种基本函数图象的分布规律(请同学们总结)
2.对数值大小的比较
(1)同底数的两个对数值的大小。由对数函数的单调性(底数 为增,
为增, 为减)比较。(2)底数不同且真数也不相同的两个对数值的大小。常用放缩法和引入中间变量法比较。(3)底数不同而真数相同的两个对数值的大小。如
为减)比较。(2)底数不同且真数也不相同的两个对数值的大小。常用放缩法和引入中间变量法比较。(3)底数不同而真数相同的两个对数值的大小。如 与
与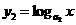 的比较(
的比较( 且
且 且
且 )。
)。
当 时,曲线
时,曲线 比
比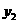 的图象(在第一象限内)上升得慢,即当
的图象(在第一象限内)上升得慢,即当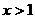 时,
时,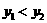 ,当
,当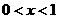 时,
时,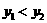 ,当
,当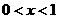 时,
时, 即在第一象限内,图象越靠近
即在第一象限内,图象越靠近 轴的对数函数底数越大。
轴的对数函数底数越大。
当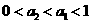 时,曲线
时,曲线 比
比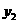 的图象(在第四象限内)下降得快,即当
的图象(在第四象限内)下降得快,即当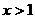 时,
时,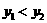 ,当
,当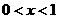 时,
时,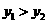 ,即在第四象限内,图象越靠近
,即在第四象限内,图象越靠近 轴的对数函数底数越小。
轴的对数函数底数越小。
1.本章中思考问题的方法
(1)指数幂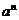 当指数扩大到有理数时,要注意底数
当指数扩大到有理数时,要注意底数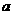 的变化范围,如当
的变化范围,如当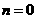 时,底数
时,底数 ;当
;当 为负整数指数时,底数
为负整数指数时,底数 ;当
;当 为分数时,底数
为分数时,底数
在掌握指数函数的图象和性质时,要对底数分两种情况讨论,即分为 与
与 两种情况。
两种情况。
(2)在对数式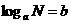 中要注意底数
中要注意底数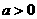 ,且
,且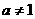 ,真数
,真数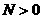 等条件,这些条件在解题或变形中常常用到。
等条件,这些条件在解题或变形中常常用到。
对数函数与指数函数互为反函数,所以它们的定义域和值域正好互换,它们的对应关系是互逆的,掌握对数函数的性质时,与掌握指数函数的性质一样,要结合它们的图象理解和记忆。
(3)掌握幂函数在第一象限内的图象特征时,要对幂指数分三种情况讨论,即分为 与
与 三种情况。
三种情况。
3.数形结合思想的运用
由于幂函数、指数函数、对数函数的图象都比较单一,也便于画出,因此利用它们的图象来比较大小,和讨论方程根的情况的题目比较普遍。
[例6]已知 ,则下列不等式中成立的一个是( )
,则下列不等式中成立的一个是( )
A.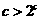 B.
B. C.
C. D.
D.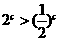
 [解析]若在同一坐标系中分别作出
[解析]若在同一坐标系中分别作出 ,
, 的图象(如图),显然
的图象(如图),显然 时,
时, 即
即 ,
,
故选C。
[点评]为比较 、
、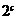 、
、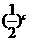 在
在 时的大小,选择什么函数是问题的关键。
时的大小,选择什么函数是问题的关键。
[例7]设函数 则不等式
则不等式 的解集是( )
的解集是( )
A.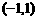 B.
B.
C. D.
D.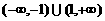
 [解析]如图,画出函数
[解析]如图,画出函数 和常函数
和常函数 的图象。若满足
的图象。若满足 ,则只需找
,则只需找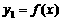 的图象在
的图象在 图象的上方所对应的
图象的上方所对应的 的取值即可。从图中很容易看出,
的取值即可。从图中很容易看出, 的解集为
的解集为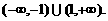
故正确答案为D。
[点评]本题也可以通过代数法求解,但是作为选择题,利用数形结合法比较简单,借助图形,不等式的解集一目了然。
[例8]方程 的实根的个数是( )
的实根的个数是( )
 A.0 B.1 C.2 D.3
A.0 B.1 C.2 D.3
[解析]分别画出函数 与
与 的图象,如图,方程
的图象,如图,方程 的实根的个数就是两个图象交点的个数。由图象可知,函数
的实根的个数就是两个图象交点的个数。由图象可知,函数 与
与 有两个交点,即方程
有两个交点,即方程 有两个实根。故正确答案为C。
有两个实根。故正确答案为C。
[点评]当方程是由两个不同类函数组成时,如果我们直接求解,但有可能无处下手,感觉到“山穷水尽”。那么,我们可以把方程的根的个数转化为两个函数的交点个数,画出两个函数的图象,交点个数便柳暗花明。
[例9]若不等式 在
在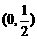 内恒成立,则
内恒成立,则 的取值范围是( )
的取值范围是( )
A.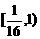 B.
B.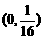 C.
C. D.
D.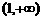
 [解析]原不等式化为
[解析]原不等式化为 ,所以不等式
,所以不等式 在
在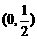 内恒成立,可转化为
内恒成立,可转化为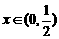 时,函数
时,函数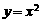 的图象在
的图象在 的图象下方,所以我们画出函数
的图象下方,所以我们画出函数 的图象下方,所以我们画出函数
的图象下方,所以我们画出函数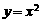 的图象,可知只有
的图象,可知只有 ,即
,即 时,才能满足
时,才能满足 在
在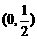 内,函数
内,函数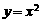 的图象恒在
的图象恒在 的图象下方,故正确答案为A。
的图象下方,故正确答案为A。
[点评]在同一个坐标系内,两个函数图象的高低体现出两个函数值的大小。因此在一定条件下,求参数范围时,我们就可以声东击西,通过比较两个函数的图象的高低,得出参数的取值范围。
[例10]对于函数 与
与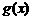 ,规定当
,规定当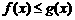 时,
时,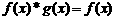 ;当
;当 时,
时,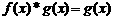 .已知
.已知 ,则
,则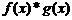 的最大值为 。
的最大值为 。
 [解析]由题意可知,
[解析]由题意可知,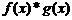 的值是两个函数
的值是两个函数 与
与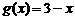 中函数值较小的那个。在同一坐标系中,分别作出函数
中函数值较小的那个。在同一坐标系中,分别作出函数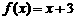 ,
,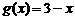 的图象。则两者中图象较低的部分就是
的图象。则两者中图象较低的部分就是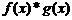 的图象,如图中实线部分,那么实线部分中最高点对应的
的图象,如图中实线部分,那么实线部分中最高点对应的 值即为
值即为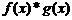 的最大值。而且,实线部分中的最高点就是两个函数图象的交点。由
的最大值。而且,实线部分中的最高点就是两个函数图象的交点。由 ,可以解得
,可以解得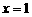 ,所以,当
,所以,当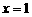 时,
时, 故
故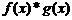 的最大值为2。
的最大值为2。
[点评]函数的最大(小)值就是函数图象最高(低)点对应的函数值。我们可以借助于图象最高点与最低点的魅力,借花献佛,巧妙转化为函数的最大(小)值。
2.分类讨论的思想
由于指数函数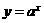 ,对数函数
,对数函数 的性质都与
的性质都与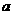 的取值范围有密切联系,
的取值范围有密切联系,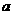 变化时函数的性质也有所变化,因此要对
变化时函数的性质也有所变化,因此要对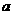 进行分类讨论。
进行分类讨论。
[例5]解方程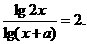
[解析]由方程可得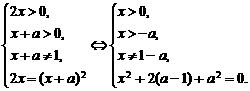
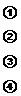
由方程④得 
当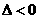 即
即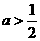 时,方程④无实数根,原方程无解。
时,方程④无实数根,原方程无解。
当 即
即 时,
时,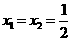 ,但不符合③,舍去。
,但不符合③,舍去。
当 即
即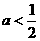 时,方程④有两根,
时,方程④有两根,
∴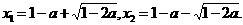
显然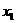 满足①②③,
满足①②③, 满足③,为使
满足③,为使 满足①②式,则
满足①②式,则

∵ 时,原方程有两解
时,原方程有两解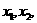
∴ 时,
时, 不满足条件①②,
不满足条件①②,
故此时,原方程只有一解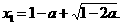
综上所述,当 时,
时,
原方程的解为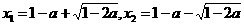 ;
;
当 时,原方程的解为
时,原方程的解为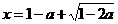 ;
;
当 时,原方程无解。
时,原方程无解。
[点评]对于二次方程④来说, 时,有两个不等实根,但对原对数方程来说,尚需满足条件①②③,因此,可能有两解,也可能有一解;
时,有两个不等实根,但对原对数方程来说,尚需满足条件①②③,因此,可能有两解,也可能有一解; 时,对二次方程④本应有相等的两个实数解,但由于条件③不满足,故对原对数方程来说又无实数解了,这种除考虑判别式外,尚需考虑条件①②③,才能确定原方程为的解的情况,必须引起注意,否则容易出错。
时,对二次方程④本应有相等的两个实数解,但由于条件③不满足,故对原对数方程来说又无实数解了,这种除考虑判别式外,尚需考虑条件①②③,才能确定原方程为的解的情况,必须引起注意,否则容易出错。
1.函数的思想
函数是描述客观世界变化规律的重要模型,不同的变化规律需要不同的函数模型描述。本章学习的三种不同类型的函数模型,刻画了客观世界中三类不同的变化规律,因而具有不同对应关系的变化现象,利用函数的意义解指数、对数方程,利用函数的单调性比较两数的大小和解指数、对数不等式是本章中运用函数思想解题的重要体现。
(1)比较大小问题
比较几个数的大小是幂、指、对函数的又一重要应用,常用的方法有:单调性法、搭桥法、图象法、特殊值法、作差法、作商法等。
[例1](1)三个数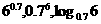 的大小顺序是( )
的大小顺序是( )
A.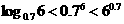 B.
B.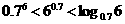
C. D.
D.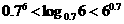
(2)比较下面两数的大小: ,
,
[解析](1)∵ ,
,
∴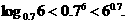
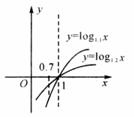
(2)注意到两个对数的真数相同,可先比较 与
与 的大小.
的大小.
 ∵
∵
∴由对数函数的单调性得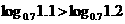 ,如图。
,如图。
又∵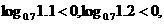
∴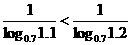 ,即
,即
另外,也可以利用对数函数图象,当底数大于1时,底数越大,在直线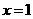 左侧图象越靠近
左侧图象越靠近 轴,由图可得,
轴,由图可得,
[答案](1)A (2)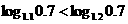
[点评](1)两个对数比较大小,须掌握以下规律:
当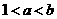 时,
时, ;当
;当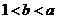 时,
时,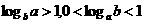 ;当
;当 时,
时, ;当
;当 时,
时,
(2)指数对数方程
指数对数方程是本章的又一重要题型,要掌握基本题型的解法及综合题的思路。
[例2]解下列方程:
(1) ;(2)
;(2)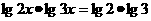 ;
;
(3)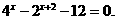
[解析]设法转化为最简单的指、对数方程进行求解。
解:(1)注意到 ,则
,则
原方程可化为
这是关于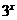 ,
,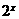 的二元齐次方程,两边除以
的二元齐次方程,两边除以 ,得
,得
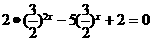 ,
,
解得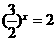 或
或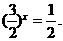
∴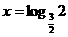 或
或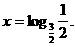
原方程的解为 或
或
(2)原方程可化为
即

解得
 或
或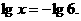
∴
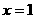 或
或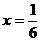 .
.
经检验,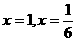 都是原方程的解。
都是原方程的解。
(3)原方程可化为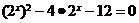
即

∴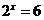 或
或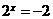 (舍).
(舍).
∴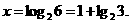
[点评]解指数、对数方程重要是运用函数思路等价转化为代数方程,要注意对数方程必须验根。
[例3]确定常数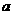 ,使方程:
,使方程:
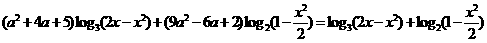 有解,并求出它的解。
有解,并求出它的解。
[解析]化简方程,从有解的必要条件入手,再考虑充分性,寻找有解的充要条件,并在此条件下求解方程。
将原方程化为同解方程
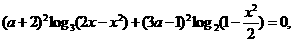
如果方程有根,则必须满足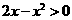 ,且
,且
解得 ,这时
,这时
即
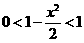 ,
,
∴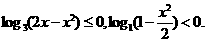
∵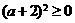 ,当
,当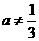 时,
时,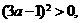
故这时,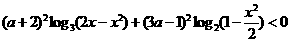 即原方程无解,为使原方程有解,必须
即原方程无解,为使原方程有解,必须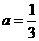 ,这即是方程有解的充要条件,当
,这即是方程有解的充要条件,当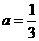 时,原方程化为
时,原方程化为 ,得
,得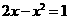 ,解得
,解得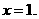
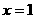 经检验是原方程的解,所以当
经检验是原方程的解,所以当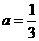 时,方程有解,其解为
时,方程有解,其解为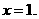
[点评]在充分运用对数函数性质的同时,还必须有严密的数学逻辑,还要运用好代数的恒等变换(方程的同解变换、配方、不等式的同解交换)。
(3)指数对数不等式
[例4]解关于 的不等式.
的不等式.
 ;
;
[解析]原不等式可化为:
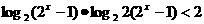 ,
,
即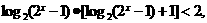
∴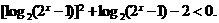
解得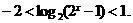
∴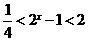 ,∴
,∴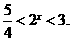
解得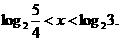
∴不等式的解集为
[点评]解方程与解不等式的过程都是不断进行同解变形的过程,它们求解的基本思路是一致的,在解方程或不等式时,总是将超越方程(或不等式)转化为代数方程(或不等式),无理转化为有理,分式转化为整式,高次转化为低次(一次或二次),在实际求解时,解方程可能通过检验完善求解过程,由于不等式的解集通常是一个区域,对解的结论不易检验,因此解不等式时,必须从一开始就注意其中字母的变化范围,使它既不扩大(消除增解的可能),也不缩小(消除失解的可能)。此外,还应注意由函数的单调性所引起的不等号的变化。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com