9．单调性的判断步骤：(1)设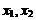是所研究区间内的任意两个自变量，且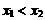；(2)判定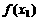与的大小；(3)作差比较或作商比较。

8．函数值域的求法：(1)配方法(二次或四次)；；(2)换元法；；(3)函数的单调性法(4)判断式法；(5)反函数法(6)不等式法

7．函数的定义域的求法：使函数有意义的自变量的不等关系式，求解即可求得函数的定义域。常涉及的依据为：(1)分母不为0；(2)偶次根式中被开方数不小于0；(3)对数的真数大于0，底数大于零且不等于1；(4)零指数幂的底数不等于零；(5)实际问题要考虑实际意义等。

6．相同函数的判定方法：(1)定义域相同；(2)对应关系相同(两点必须同时具备)。

5．若集合中含有参数，须对参数进行分类讨论，讨论时要不重不漏。

4．若集合中的元素是用坐标形式给出的，要注意满足条件的点构成的图形是什么，用数形结合法解之。

3．在集合运算中必须注意组成集合的元素应具备的性质。

2．在判定给定对象能否构成集合时，特别要注意它的“确定性”；在表示一个集合时，要特别注意它的“互异性”。

1．正确理解集合的概念必须掌握构成集合的两个必要条件：研究对象是具体的，其属性是确定的。

4．等价转化的思想

数学问题中，已知条件是结论成立的保证。但有的问题已知条件和结论之间，距离比较大，难于解出。因此，如何将已知条件经过转化，逐步向需求结论靠拢，这就是解题过程中经常要做的工作。变更条件就是利用与原条件等价的条件去代替，使得原条件中的隐含的因素显露出来，使各种关系明朗化，从而缩短已知条件和结论之间的距离，找出它们之间内在联系，以便应用数学规律、方法将问题予以解决。

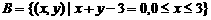［例］已知集合与,若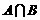为单元素集合。求实数的取值范围。

［解析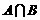］为单元素集合，等价于不等式组

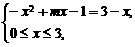有唯一一组解。

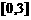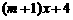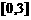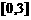即，此方程在上有一实根或两相等实根，设 ，且的图象与轴相切于区间上或与轴相交，且只能一个交点落在区间上，于是有

若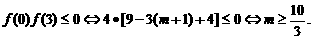

综上所述，实数的取值范围是或

［点评］将集合问题转化为方程根的讨论问题，若利用求根公式解之，则较为繁锁，设，则方程在区间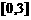上有两相等的实根，等价于函数的图象与轴相切，且顶点落在区间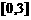上；这样，方程根的讨论问题就转化为二次函数图象与轴交点的讨论问题，从而问题得以解决。