
题目列表(包括答案和解析)
4. 同角三角函数基本关系式
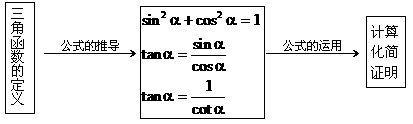
(1)根据一个角的某一三角函数值求其它的三角函数值。需注意先用平方关系,后用商数关系,最后用倒数关系,关键注意符号问题。
(2)三角函数式的化简,注意化简的结果做到“五个尽量”,即①项数尽量少,②次数尽量低,③尽量不含分母,④尽量不带根号,⑤尽量化为数值。
(3)三角恒等式的证明,掌握常规的化弦法(即:切割化弦)以及由繁到简法等。
3. 任意角的三角函数
(1)三角函数的概念:
设α是一个任意角,α的终边上任意一点P的坐标是(x,y),它与原点的距离为r,三个量的六种比值是:
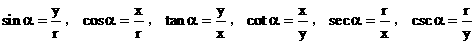
这六种比值分别叫做α的正弦、余弦、正切、余切、正割、余割。这种以角为自变量,以比值为函数值的函数,统称为三角函数。由于角α终边确定,由几何知识知,这六个比值与P点在α终边上的位置无关。
(2)三角函数线
借助三角函数定义,可用单位圆中的有向线段MP,OM,AT等分别表示α角的正弦,余弦,正切。可见三角函数线是三角函数定义的形象表示。(注意课本上字母的确定位置。)
(3)三角函数值以及符号
由于用角α终边上点的坐标来定义三角函数,因此,由点的坐标的符号,就可以决定α的六个三角函数值符号。
(4)终边相同的三角函数值
由三角函数的定义知:终边相同的角的同一三角函数值相同。即:
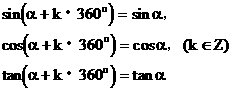
它可以把求任意角的三角函数值转化为求0°到360°之间角的三角函数值。
2. 弧度制
(1)把长度等于半径长的弧所对的圆心角叫1弧度的角。这种以弧度作为单位来度量角的单位制,叫做弧度制。
(2)弧度制的意义:首先是定义三角函数及绘制三角函数图象的需要,其次弧度数是实数,它把角集合与实数集合之间建立了一一对应关系,再次可简化弧长公式与扇形面积公式。
(3)角度制与弧度制的换算:180°=πrad是角度与弧度换算公式的基础,这里π是圆周率,应注意π≠3.14,π≠1 rad。
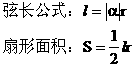
1. 角的概念的推广
(1)角的概念、正角、负角、零角的概念。在这些概念中要注意旋转的方向。
(2)象限角的概念,这个概念的前提是这个角的顶点与坐标原点重合,角的始边与x轴非负半轴重合。在这个前提下,才能由终边所在象限来判定某角为第几象限角。在上述前提下,如果某角的终边在坐标轴上,就认为这个角不属于任一象限。
①会表示象限角、区间角、终边相同的角及其它特殊角。
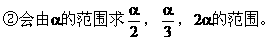
(3)终边相同角的统一记法,与角α终边相同的角的一般形式为α+k·360°。要注意:①k∈Z;②α是任意角;③终边相同的角不一定相等,但相等的角的终边一定相同。终边相同的角有无限多个,它们相差360°的整数倍。
三角函数
8. 如图,已知
如图,已知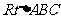 ,
, 是斜边AB的中点,过
是斜边AB的中点,过 作
作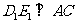 于
于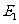 ,连接
,连接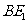 交
交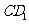 于
于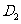 ,过
,过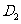 作
作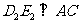 于
于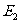 ,连接
,连接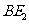 交
交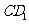 于
于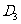 ,过
,过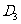 作
作 于
于 ……如此继续,可以依次得到点
……如此继续,可以依次得到点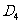 ,
,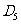 ,
,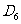 …
… ,分别记
,分别记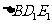 ,
,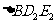 …
… 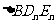 的面积为
的面积为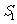 ,
,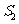 …
…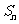 ,则
,则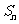 =( )
=( )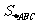 .(用含n的代数式表示)
.(用含n的代数式表示)
7.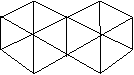 如图是由12个边长相等的正三角形镶嵌而成的平面图形,
如图是由12个边长相等的正三角形镶嵌而成的平面图形,
则图中的平行四边形共有 个.
6.如图,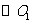 和
和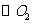 的半径分别是1和3,连结
的半径分别是1和3,连结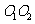 ,交
,交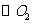
于点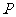 ,
,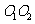 =8,若将
=8,若将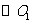 绕点
绕点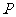 按顺时针方向旋转
按顺时针方向旋转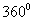 ,
,
则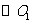 与
与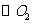 共相切 次.
共相切 次.
5. 在平面直角坐标系中,有
在平面直角坐标系中,有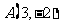 ,
,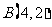 两点,现另取一点
两点,现另取一点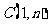 ,当n= 时,
,当n= 时,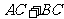 的值最小.
的值最小.
4.设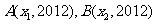 是二次函数
是二次函数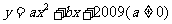 的图像上的两点,则当
的图像上的两点,则当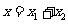 时二次函数的值为
.
时二次函数的值为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com