
题目列表(包括答案和解析)
2、一元二次方程与二次函数的关系。
1、二次函数的三种表示方法:(1)一般式 (2)顶点式
(2)顶点式
(3)两点式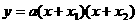
(三)、同步练习:
1、下列各函数解析式中,满足 的是 ( )
的是 ( )
(A) 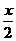 (B)
(B) (C)
(C) 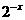 (D)
(D)
答案:C
2、已知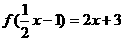 ,且
,且 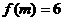 ,则
,则 等于
( )
等于
( )
(A) 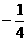 (B)
(B) (C)
(C) 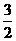 (D)
(D)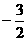
答案:A
3、已知 ,则函数
,则函数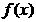 的解析式为
( )
的解析式为
( )
(A) (B)
(B)
(C) (D)
(D)
答案:C
4、已知 ,则
,则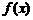 的解析式可取为
的解析式可取为 等于( )
等于( )
A. B.
B.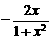 C.
C. D.
D.
答案:C
5.设函数 若
若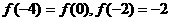 则关于x的方程
则关于x的方程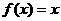 的解的个数为( )
的解的个数为( )
(A)1 (B)2 (C)3 (D)4
答案:C
6、若函数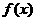 满足关系式
满足关系式 ,则
,则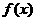 的表达式为__________
的表达式为__________
答案:
7、设函数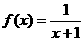 的图象为
的图象为 ,若函数
,若函数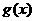 的图象
的图象 与
与 关于
关于 轴对称,则
轴对称,则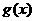 的解析式为________________.
的解析式为________________.
答案: 、
、
8、若一次函数y=f (x)在区间 上的最大值为3,最小值为1,则y=f (x)的解析式为_____________.
上的最大值为3,最小值为1,则y=f (x)的解析式为_____________.
答案: 或
或
9、已知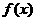 是奇函数,
是奇函数,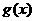 是偶函数,且
是偶函数,且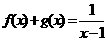 ,则
,则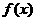 = ___
= ___
答案: 
10、二次函数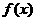 满足
满足 ,且
,且 。⑴ 求
。⑴ 求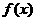 的解析式;
的解析式;
⑵ 在区间 上,
上,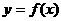 的图象恒在
的图象恒在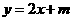 的上方,试确定
的上方,试确定 的范围。
的范围。
答案(1) (2)
(2)
11、已知 ,当点
,当点 在函数
在函数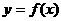 的图象上运动时,点
的图象上运动时,点 在 函数
在 函数 的图象上运动
的图象上运动
(1)
写出 的解析式;
的解析式;
(2)
求出使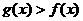 的x 的取值范围;
的x 的取值范围;
(3)
在(2)的范围内,求 的最大值。
的最大值。
答案:(1)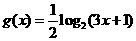 (2)
(2)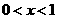 (3)
(3)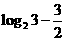
第四篇 二次函数问题
(二)、例题演练:
例1、求下列函数的解析式:
(1)已知 ,求
,求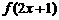 ;
;
(2)已知 ,求
,求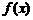 ;
;
(3)已知 ,求
,求
[解析](1)
(2)解法一(拼凑法): ,而
,而 故所求的函数
故所求的函数
解法二(换元法):令 ,则
,则 ,
,
∴
故所求的函数为
(3)令 ,则
,则 ,∴
,∴ ,
,
即 .与原式联立,得
.与原式联立,得
 解得
解得
∴所求的函数为
[点评]由 的解析式,求出函数
的解析式,求出函数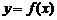 后,应注意函数的定义域。此时
后,应注意函数的定义域。此时 的取值不仅要使
的取值不仅要使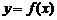 有意义,同时还要使
有意义,同时还要使 也有意义,也就是
也有意义,也就是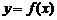 的定义域包含于
的定义域包含于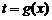 的值域之中。
的值域之中。
例2、设二次函数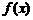 满足
满足 ,且图象在
,且图象在 轴上的截距为1,被
轴上的截距为1,被 截得的线段长为
截得的线段长为 ,求
,求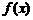 的解析式。
的解析式。
[解析]解法一:设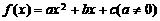 .由
.由 得
得 ①;
①;
又 ,∴
,∴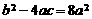 ②;
②;
又由已知得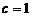 ③;
③;
由①②③得
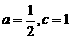 ,∴
,∴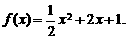
解法二: ,故
,故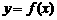 的图象有对称轴
的图象有对称轴 ,可设依题意可设设
,可设依题意可设设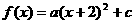 ,有
,有

解法三:∵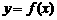 的图象有对称轴
的图象有对称轴 ,又
,又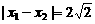 ,
,
∴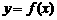 与
与 轴的交点为
轴的交点为
故可设
∵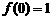 ,∴
,∴ (其余略)。
(其余略)。
[点评]三种方法均是待定系数法求二次函数的解析式,可以得到充分挖掘题目的隐含条件及充分利用图形的直观性,是简化运算的有效手段。
[例3]设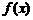 是R上的函数,且满足
是R上的函数,且满足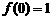 ,并且对任意实数
,并且对任意实数 、
、 有
有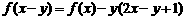 ,求
,求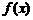 的表达式。
的表达式。
[解]解法一:由 ,
,
设 ,得
,得
∵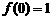 ,∴
,∴ ,
,
即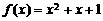 。
。
又令 ,代入上式得
,代入上式得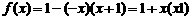 ,
,
∴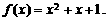
[点 评]:赋值法(亦称特殊值法),可以取特殊值,亦可以是变量换变量,然后通过解方程组求出参数。
例4、(1)已知 ,且
,且 ,求
,求
(2)已知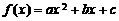 ,若
,若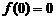 ,且
,且 ,试求
,试求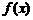 的表达式。
的表达式。
[解析](1)∵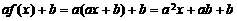 ,
,
∴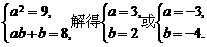
∴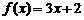 或
或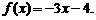
(2)∵ ,∴
,∴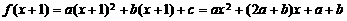 ,
,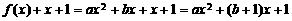 ,
,
∴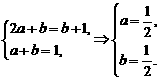 ∴
∴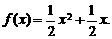
[点评]此题通过待定系数法来求函数的解析式。这是已知函数类型求其解析式的常用方法。
例5、已知函数 与
与 的图象关于点(--2,3)对称,求
的图象关于点(--2,3)对称,求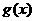 的解析式。
的解析式。
解:设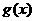 上任意一点为
上任意一点为 ,则
,则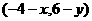 在
在 上,代入整理得
上,代入整理得
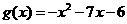
(一)、知识回顾:
1、求函数解析式的常用方法:
ⅰ、换元法( 注意新元的取值范围)
ⅱ、待定系数法(已知函数类型如:一次、二次函数、反比例函数等)
ⅲ、整体代换(配凑法)
ⅳ、构造方程组(如自变量互为倒数、已知f(x)为奇函数且g(x)为偶函数等)
2、求函数的解析式应指明函数的定义域,函数的定义域是使式子有意义的的取值范围,同时也要注意变量的实际意义。
3、理解轨迹思想在求对称曲线中的应用。
1:如图所示,单位圆中弧AB的长为 表示弧AB与弦AB
表示弧AB与弦AB
所围成的弓形面积的2倍,则函数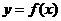 的图象是
的图象是
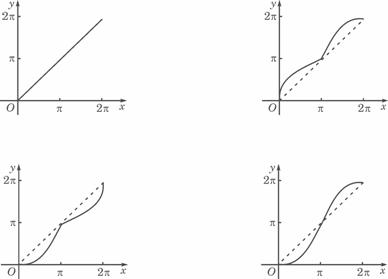
答案:( D )
设计意图:考察图象与式子运算的能力
2、为了稳定市场,确保农民增收,某农产品的市场收购价格 与其前三个月的市场收购价格有关,且使
与其前三个月的市场收购价格有关,且使 与其前三个月的市场收购价格之差的平方和最小.若下表列出的是该产品前6个月的市场收购价格:
与其前三个月的市场收购价格之差的平方和最小.若下表列出的是该产品前6个月的市场收购价格:
|
月份 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
价格(元/担) |
68 |
78 |
67 |
71 |
72 |
70 |
|
则7月份该产品的市场收购价格应为 ( )
A.69元 B.70元 C.71元 D.72元
答案:C
3、已知函数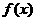 是
是 上的增函数,
上的增函数, 是其函数图象上的两点,那么
是其函数图象上的两点,那么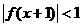 的解集的补集是:( )
的解集的补集是:( )
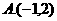



答案:D
4、方程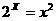 的实根的个数为( )A:0
B:1 C:2 D:3
的实根的个数为( )A:0
B:1 C:2 D:3
答案D
5.为了得到函数 的图象,可以把函数
的图象,可以把函数 的图象( )
的图象( )
A.向左平移3个单位长度 B.向右平移3个单位长度
C.向左平移1个单位长度 D.向右平移1个单位长度
[解析]∵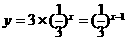 ,∴由
,∴由 的图象向右平移1个单位长度。
的图象向右平移1个单位长度。
6.已知函数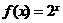 ,则
,则 的图象为图中的( )
的图象为图中的( )
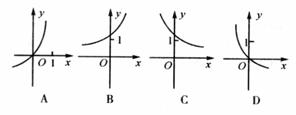
[解析] ,这是把函数
,这是把函数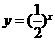 的图象向右平移1个单位而得。
的图象向右平移1个单位而得。
故选C。
7。要得到 的图像,只需作
的图像,只需作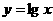 关于_____轴对称的图像,再向____平移3个单位而得到。
关于_____轴对称的图像,再向____平移3个单位而得到。
答案: 轴,右
轴,右
8。已知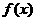 是偶函数,则
是偶函数,则 的图像关于__________对称;已知
的图像关于__________对称;已知 是偶函数,则函数
是偶函数,则函数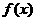 的图像关于____________对称.
的图像关于____________对称.
答案:直线 ;直线
;直线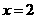
9、写出函数 的图像经过怎样的变换可得到函数
的图像经过怎样的变换可得到函数 的图像。
的图像。
答案、左移1个单位
10、 若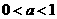 ,则方程
,则方程 有几个实根
有几个实根
答案:(1) 2个
11、设曲线C的方程是 ,将C沿x轴,y轴正方向分别平行移动t,s单位长度后得曲线
,将C沿x轴,y轴正方向分别平行移动t,s单位长度后得曲线 。 (1)写出曲线
。 (1)写出曲线 的方程;(2)证明曲线C与
的方程;(2)证明曲线C与 关于点
关于点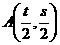 对称
对称
答案:(1) (2)略
(2)略
12、将函数 的图像沿x轴向右平移1个单位,得到图像C,图像C1与C关于原点对称,图像C2与C1关于直线y=x对称,求C2对应的函数。
的图像沿x轴向右平移1个单位,得到图像C,图像C1与C关于原点对称,图像C2与C1关于直线y=x对称,求C2对应的函数。
答案、
13、试讨论方程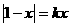 的实数根的个数。
的实数根的个数。
答案、 时有一解;当
时有一解;当 时有二解;当
时有二解;当 无解
无解
14、设a是常数,函数f(x)对一切实数x都满足 ,求证函数f(x)的图像关于点(a,0)成中心对称图形。
,求证函数f(x)的图像关于点(a,0)成中心对称图形。
答案:略
第三篇 函数的解析式问题
(二)例题演练:
例1.函数 的图象是( )
的图象是( )
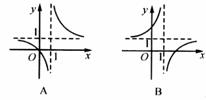

[解析]该题考查对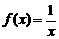 图象以及坐标平移公式的理解,将函数
图象以及坐标平移公式的理解,将函数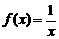 的图象变形到
的图象变形到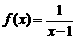 ,即向右平移一个单位,再变形到
,即向右平移一个单位,再变形到 ,即将前面图象沿
,即将前面图象沿 轴翻转,再变形到
轴翻转,再变形到 ,即将前面图象再向上平移一个单位,从而得到答案B。
,即将前面图象再向上平移一个单位,从而得到答案B。
例2.如图所示, 是定义在
是定义在 上的四个函数,其中满足性质:“对
上的四个函数,其中满足性质:“对 中任意的
中任意的 和
和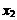 ,
, 恒成立”的只有( )
恒成立”的只有( )
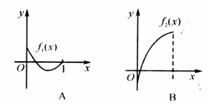

[解析]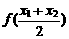 为自变量
为自变量 的中点,
的中点,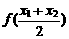 对应的函数值即“中点的纵坐标”,
对应的函数值即“中点的纵坐标”,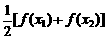 为自变量
为自变量 对应的函数值所对应的点的中点,即“纵坐标的中点”。再结合
对应的函数值所对应的点的中点,即“纵坐标的中点”。再结合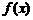 函数图象的凹凸性,可得到答案A,这是函数凹凸性的基本应用。故选A。
函数图象的凹凸性,可得到答案A,这是函数凹凸性的基本应用。故选A。
例3、利用函数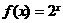 的图象,作出下列各函数的图象:
的图象,作出下列各函数的图象:
(1) ;(2)
;(2)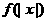 ;(3)
;(3) ;(4)
;(4)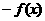 ;(5)
;(5)
[解析]利用指数函数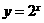 的图象及变换作图法可作要作的函数图象,其图象如图(1)-(5)中的实线部分。
的图象及变换作图法可作要作的函数图象,其图象如图(1)-(5)中的实线部分。

[例4]已知 ,且
,且 1,函数
1,函数 与
与 的图象只能是图中的( )
的图象只能是图中的( )
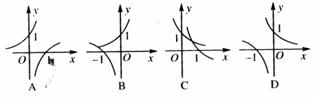
[分析]可以从图象所在的位置及单调性来判别,也可利用函数的性质识别图象,特别注意底数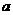 对图象的影响。
对图象的影响。
解法一:首先,曲线 只可能在上半平面,
只可能在上半平面, 只可能在左半平面上,从而排除A、C。
只可能在左半平面上,从而排除A、C。
其次,从单调性着眼, 与
与 的增减性正好相反,又可排除D。
的增减性正好相反,又可排除D。
解法二:若 ,则曲线
,则曲线 下降且过点(0,1),而曲线
下降且过点(0,1),而曲线 上升且过
上升且过 ,以上图象均不符合这些条件. 若
,以上图象均不符合这些条件. 若 时,则曲线
时,则曲线 上升且过(0,1),而曲线
上升且过(0,1),而曲线 下降且过
下降且过 ,只有B满足条件。
,只有B满足条件。
解法三:如果注意到 的图象关于
的图象关于 轴的对称图象为
轴的对称图象为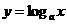 ,又
,又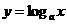 与
与 互为反函数(图象关于直线
互为反函数(图象关于直线 对称),则可直接选定B。
对称),则可直接选定B。
[答案]B
[例5]作出 的图象.
的图象.
[分析]利用图象变换作图(如图)
[解析]第一步:作出 的图象(图①).
的图象(图①).
第二步:将 的图象沿
的图象沿 轴向左平移1个单位得
轴向左平移1个单位得 的图象(图②).
的图象(图②).
第三步:将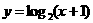 的图象在
的图象在 轴下方的图象,以
轴下方的图象,以 轴为对称轴对称到
轴为对称轴对称到 轴的上方得
轴的上方得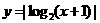 的图象)(图③).
的图象)(图③).
第四步:将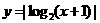 的图象沿
的图象沿 轴方向向上平移2个单位,得到
轴方向向上平移2个单位,得到 的图象(图④).
的图象(图④).
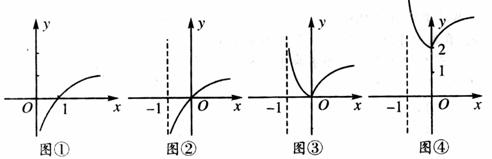
[点评](1)一般地,函数 的图象可由函数
的图象可由函数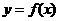 的图象变换得到。
的图象变换得到。
将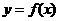 的图象向左或向右平移
的图象向左或向右平移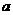 个单位可得到函数
个单位可得到函数 的图象,向下或向上平移
的图象,向下或向上平移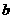 个单位可得到函数
个单位可得到函数 的图象(记忆口诀:上加下减)。
的图象(记忆口诀:上加下减)。
(2)含有绝对值的函数的图象变换是一种对称变换,一般地, 的图象是关于
的图象是关于 对称的轴对称图形;函数
对称的轴对称图形;函数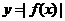 的图象与
的图象与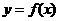 的图象在
的图象在 轴上方相同,在
轴上方相同,在 轴下方关于
轴下方关于 轴对称。
轴对称。
 (3)
(3)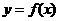 的图象
的图象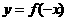 的图象关于
的图象关于 轴对称,
轴对称,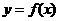 的图象与
的图象与 的图象关于
的图象关于 轴对称。
轴对称。
[例6]函数 与函数
与函数 的图象如右,则函数
的图象如右,则函数 ·
·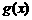 的图象是( )
的图象是( )

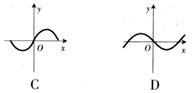
[解析]由图象可知,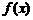 是偶函数,
是偶函数,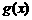 是奇函数,且
是奇函数,且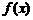 与
与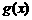 的公共定义域为
的公共定义域为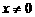 ,排除C、D。令
,排除C、D。令 ·
·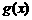 ,则
,则 ·
·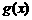 ,所以
,所以 为奇函数,其图象关于原点对称,排除B。故选A。
为奇函数,其图象关于原点对称,排除B。故选A。
(一)知识方法
1.用描点法作函数的图象.
2.正比例函数、反比例函数、二次函数的图象及几种基本初等函数的图象.
3.图象变换与变量替换的关系
(1)平移变换((2)变换作图法:
①平移:
 ;
;
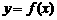


②对称: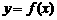

 ;
;
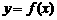

 ;
;
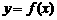

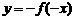 .
.
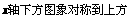 ③其他:
③其他: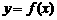

 ;
;

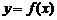


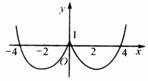 [例]作函数
[例]作函数 的图象时,先用虚线作
的图象时,先用虚线作 的图象,再保留
的图象,再保留 轴右边图象,并把它对称翻到
轴右边图象,并把它对称翻到 轴左边,即得到
轴左边,即得到 的图象,如图所示。
的图象,如图所示。
4.作函数图像的一般步骤是:
(1)求出函数的定义域;(2)化简函数式;(3)讨论函数的性质(如奇偶性、周期性、单调性)以及图像上的特殊点、线(如极值点、渐近线、对称轴等);(4)利用基本函数的图像画出所给函数的图像。
(1)引理证明
已知函数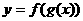 .若
.若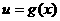 在区间
在区间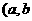 )上是减函数,其值域为(c,d),又函数
)上是减函数,其值域为(c,d),又函数 在区间(c,d)上是减函数,那么,原复合函数
在区间(c,d)上是减函数,那么,原复合函数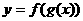 在区间
在区间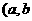 )上是增函数.
)上是增函数.
证明:在区间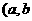 )内任取两个数
)内任取两个数 ,使
,使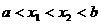
因为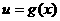 在区间
在区间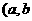 )上是减函数,所以
)上是减函数,所以 ,记
,记 ,
, 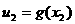 即
即
因为函数 在区间(c,d)上是减函数,所以
在区间(c,d)上是减函数,所以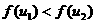 ,即
,即 ,
,
故函数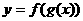 在区间
在区间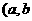 )上是增函数.
)上是增函数.
(2).复合函数单调性的判断
复合函数的单调性是由两个函数共同决定。为了记忆方便,我们把它们总结成一个图表:
 |
增 ↗ |
减 ↘ |
||
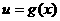 |
增 ↗ |
减 ↘ |
增 ↗ |
减 ↘ |
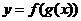 |
增 ↗ |
减 ↘ |
减 ↘ |
增 ↗ |
以上规律还可总结为:“同向得增,异向得减”或“同增异减”.
(3)、复合函数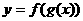 的单调性判断步骤:
的单调性判断步骤:
ⅰ 确定函数的定义域;
ⅱ 将复合函数分解成两个简单函数: 与
与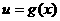 。
。
ⅲ 分别确定分解成的两个函数的单调性;
ⅳ 若两个函数在对应的区间上的单调性相同(即都是增函数,或都是减函数),则复合后的函数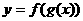 为增函数; 若两个函数在对应的区间上的单调性相异(即一个是增函数,而另一个是减函数),则复合后的函数
为增函数; 若两个函数在对应的区间上的单调性相异(即一个是增函数,而另一个是减函数),则复合后的函数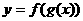 为减函数。
为减函数。
(4)例题演练
例1、 求函数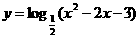 的单调区间,并用单调定义给予证明
的单调区间,并用单调定义给予证明
解:定义域 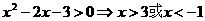
单调减区间是 设
设 则
则



 =
=
∵ ∴
∴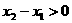

∴ >
> 又底数
又底数
∴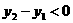 即
即 
∴ 在
在 上是减函数
上是减函数
同理可证: 在
在 上是增函数
上是增函数
[例]2、讨论函数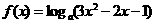 的单调性.
的单调性.
[解]由 得函数的定义域为
得函数的定义域为

则当 时,若
时,若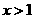 ,∵
,∵ 为增函数,∴
为增函数,∴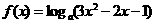 为增函数.
为增函数.
若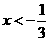 ,∵
,∵ 为减函数.
为减函数.
∴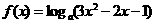 为减函数。
为减函数。
当 时,若
时,若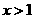 ,则
,则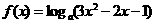 为减函数,若
为减函数,若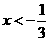 ,则
,则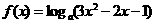 为增函数.
为增函数.
例3、.已知y= (2-
(2-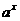 )在[0,1]上是x的减函数,求a的取值范围.
)在[0,1]上是x的减函数,求a的取值范围.
解:∵a>0且a≠1
当a>1时,函数t=2-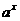 >0是减函数
>0是减函数
由y= (2-
(2-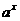 )在[0,1]上x的减函数,知y=
)在[0,1]上x的减函数,知y= t是增函数,
t是增函数,
∴a>1
由x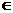 [0,1]时,2-
[0,1]时,2-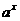
 2-a>0,得a<2,
2-a>0,得a<2,
∴1<a<2
当0<a<1时,函数t=2-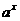 >0是增函数
>0是增函数
由y= (2-
(2-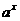 )在[0,1]上x的减函数,知y=
)在[0,1]上x的减函数,知y= t是减函数,
t是减函数,
∴0<a<1
由x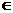 [0,1]时,2-
[0,1]时,2-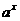
 2-1>0, ∴0<a<1
2-1>0, ∴0<a<1
综上述,0<a<1或1<a<2
例4、已知函数 (
(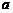 为负整数)的图象经过点
为负整数)的图象经过点 ,设
,设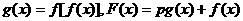 .问是否存在实数
.问是否存在实数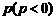 使得
使得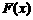 在区间
在区间 上是减函数,且在区间
上是减函数,且在区间 上是减函数?并证明你的结论。
上是减函数?并证明你的结论。
[解析]由已知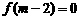 ,得
,得 ,
,
其中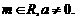 ∴
∴ 即
即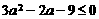 ,
,
解得
∵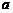 为负整数,∴
为负整数,∴
∴ ,
,
即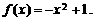
 ,
,
∴
假设存在实数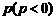 ,使得
,使得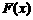 满足条件,设
满足条件,设 ,
,
∴
∵ ,当
,当 时,
时,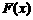 为减函数,
为减函数,
∴ ,∴
,∴
∵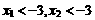 ,∴
,∴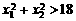 ,
,
∴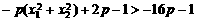 ,
,
∴ ①
①
当 时,
时,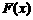 增函数,∴
增函数,∴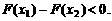
∵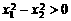 ,∴
,∴ ,
,
∴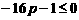 . ②
. ②
由①、②可知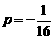 ,故存在
,故存在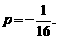
(5)同步练习:
1.函数y= (x2-3x+2)的单调递减区间是( )
(x2-3x+2)的单调递减区间是( )
A.(-∞,1) B.(2,+∞)
C.(-∞,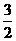 ) D.(
) D.(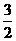 ,+∞)
,+∞)
解析:先求函数定义域为(-o,1)∪(2,+∞),令t(x)=x2+3x+2,函数t(x)在(-∞,1)上单调递减,在(2,+∞)上单调递增,根据复合函数同增异减的原则,函数y= (x2-3x+2)在(2,+∞)上单调递减.
(x2-3x+2)在(2,+∞)上单调递减.
答案:B
2找出下列函数的单调区间.
(1)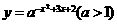 ;
;
(2)
答案:(1)在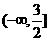 上是增函数,在
上是增函数,在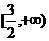 上是减函数。
上是减函数。
(2)单调增区间是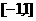 ,减区间是
,减区间是 。
。
3、讨论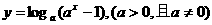 的单调性。
的单调性。
答案: 时
时 为增函数,
为增函数,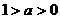 时,
时, 为增函数。
为增函数。
4.求函数y= (x2-5x+4)的定义域、值域和单调区间.
(x2-5x+4)的定义域、值域和单调区间.
解:由 (x)=x2-5x+4>0,解得x>4或x<1,所以x∈(-∞,1)∪(4,+∞),当x∈(-∞,1)∪(4,+∞),{
(x)=x2-5x+4>0,解得x>4或x<1,所以x∈(-∞,1)∪(4,+∞),当x∈(-∞,1)∪(4,+∞),{ |
| =x2-5x+4}=R+,所以函数的值域是R+.因为函数y=
=x2-5x+4}=R+,所以函数的值域是R+.因为函数y= (x2-5x+4)是由y=
(x2-5x+4)是由y=
 (x)与
(x)与 (x)=x2-5x+4复合而成,函数y=
(x)=x2-5x+4复合而成,函数y=
 (x)在其定义域上是单调递减的,函数
(x)在其定义域上是单调递减的,函数 (x)=x2-5x+4在(-∞,
(x)=x2-5x+4在(-∞, )上为减函数,在[
)上为减函数,在[ ,+∞]上为增函数.考虑到函数的定义域及复合函数单调性,y=
,+∞]上为增函数.考虑到函数的定义域及复合函数单调性,y= (x2-5x+4)的增区间是定义域内使y=
(x2-5x+4)的增区间是定义域内使y=
 (x)为减函数、
(x)为减函数、 (x)=x2-5x+4也为减函数的区间,即(-∞,1);y=
(x)=x2-5x+4也为减函数的区间,即(-∞,1);y= (x2-5x+4)的减区间是定义域内使y=
(x2-5x+4)的减区间是定义域内使y=
 (x)为减函数、
(x)为减函数、 (x)=x2-5x+4为增函数的区间,即(4,+∞).
(x)=x2-5x+4为增函数的区间,即(4,+∞).
第二篇 函数图象问题
数形结合是中学数学的重要的数学思想方法,尤其是函数的图象更是历年高考的热点.函数图象是函数的一种表达形式,形象的显示了函数的性质,为研究数量关系提供了“形”的直观性,它是探求解题途径,获得问题的结果的重要工具.
(二)同步练习:
1、 已知函数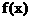 的定义域为
的定义域为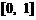 ,求函数
,求函数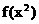 的定义域。
的定义域。
答案: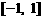
2、 已知函数 的定义域为
的定义域为 ,求
,求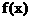 的定义域。
的定义域。
答案:
3、 已知函数 的定义域为
的定义域为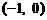 ,求
,求 的定义域。
的定义域。
答案:
4、设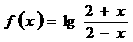 ,则
,则 的定义域为( )
的定义域为( )
A.  B.
B.
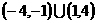
C. 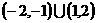 D.
D. 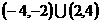
解:选C.由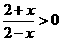 得,
得,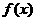 的定义域为
的定义域为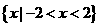 。故
。故 ,解得
,解得 。故
。故 的定义域为
的定义域为
5、已知函数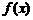 的定义域为
的定义域为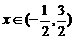 ,求
,求 的定义域。
的定义域。
[解析]由已知,有
(1)当 时,定义域为
时,定义域为 ;
;
(2)当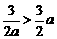 ,即
,即 时,有
时,有 ,
,
定义域为 ;
;
(3)当 ,即
,即 时,有
时,有 ,
,
定义域为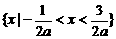 .
.
故当 时,定义域为
时,定义域为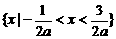 ;
;
当 时,定义域为
时,定义域为
[点评]对于含有参数的函数,求其定义域,必须对字母进行讨论,要注意思考讨论字母的方法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com