
题目列表(包括答案和解析)
5. 设g(x)为R上不恒等于0的奇函数, (a>0且a≠1)为偶函数,则常数b的值为 ( )
(a>0且a≠1)为偶函数,则常数b的值为 ( )
A.2 B.1 C. D.与a有关的值
D.与a有关的值
4.北京市为成功举办2008年奥运会,决定从2003年到2007年五年间更新市内现有的全部出租车,若每年更新的车辆数比前一年递增10%,则2003年底更新现有总车辆数的(参考数据:1.14=1.46,1.15=1.61) ( )
A.10% B.16.4% C.16.8% D.20%
3.函数 当x>2 时恒有
当x>2 时恒有 >1,则a的取值范围是 ( )
>1,则a的取值范围是 ( )
A.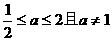 B.0
B.0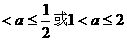 C.
C. D.
D.
2、已知 ,则
,则 ( )
( )
A、 B、
B、 C、
C、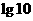 D、
D、
1.已知p>q>1,0<a<1,则下列各式中正确的是 ( )
A. B.
B. C.
C. D.
D.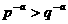
19.解:(1)因为0<c<1,所以c2<c.
由f(c2)=,得c3+1=,c=.
(2)由(1)得f(x)=
由f(x)>+1可知,
当0<x<时,x+1>+1,
解得<x<;
当≤x<1时,2-4x+1>+1,解得≤x<,
所以f(x)>+1的解集为{x|<x<}.
18.解:(1)由对数的意义,分别得1+x>0,1-x>0,即x>-1,x<1.∴函数f(x)的定义域为(-1,+∞),函数g(x)的定义域为(-∞,1),
∴函数h(x)的定义域为(-1,1).
(2)∵对任意的x∈(-1,1),-x∈(-1,1),
h(-x)=f(-x)-g(-x)
=loga(1-x)-loga(1+x)
=g(x)-f(x)=-h(x),
∴h(x)是奇函数.
(3)由f(3)=2,得a=2.
此时h(x)=log2(1+x)-log2(1-x),
由h(x)>0即log2(1+x)-log2(1-x)>0,
∴log2(1+x)>log2(1-x).
由1+x>1-x>0,解得0<x<1.
故使h(x)>0成立的x的集合是{x|0<x<1}.
17.解:(1)光线经过1块玻璃后强度为(1-10%)·k=0.9k;
光线经过2块玻璃后强度为(1-10%)·0.9k=0.92k;
光线经过3块玻璃后强度为(1-10%)·0.92k=0.93k;
光线经过x块玻璃后强度为0.9xk.
∴y=0.9xk(x∈N*).
(2)由题意0.9xk<,∴0.9x<.
两边取对数,xlg0.9<lg.
∵lg0.9<0,∴x>.
∵≈10.4,∴xmin=11,即通过11块玻璃以后,光线强度减弱到原来的以下.
16.解:(1)f(a)+f(1-a)=+
=+=+
=+==1.
(2)f()+f()+f()+…+f()=[f()+f()]+[f()+f()]+…+[f()+f()]=500×1=500.
15.解:由题意可知,α+β=,αβ=2.于是α2-αβ+β2=(α+β)2-3αβ=10-6=4,(α-β)2=(α+β)2-4αβ=10-8=2.
所以,原式=log4=.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com