
题目列表(包括答案和解析)
1.下列各项中,不可以组成集合的是( )
A.所有的正数 B.等于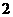 的数
的数
C.接近于 的数 D.不等于
的数 D.不等于 的偶数
的偶数
例6 用 ,
, 填空
填空

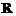
错解:
错误的原因在于没有弄清符号“ ”与“
”与“ ”之间的区别
”之间的区别
“ ”表示元素与集合之间的关系,“
”表示元素与集合之间的关系,“ ”表示集合与集合之间的关系,
”表示集合与集合之间的关系, 表示集合,
表示集合,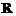 亦是集合,
亦是集合,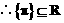 .
.
例5 若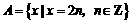 ,
, ,试问
,试问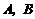 是否相等.
是否相等.
错解: 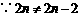
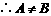
剖析:只看到两集合的形式区别,没有弄清事物的本质,事实上 是偶数集,
是偶数集,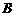 也是偶数集,两集合应相等,尽管形式不同.
也是偶数集,两集合应相等,尽管形式不同.

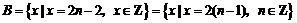
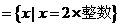
换句话说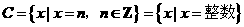 ,
,

两集合中所含元素完全相同,
例4 设全集 ,
,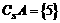 ,求
,求 的值.
的值.
错解: 
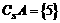
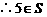 且
且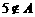

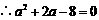
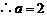 或
或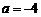
剖析:没有正确理解全集的含义,产生增解的错误.全集中应含有讨论集合中的一切元素,所以还须检验.
(1)当 时,
时,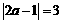 ,此时满足
,此时满足 .
.
(2)当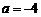 时,
时, ,
,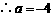 应舍去,
应舍去,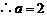 .
.
例3 已知集合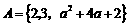 ,
,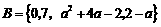 ,且
,且 ,求
,求 的值.
的值.
错解: 
 ,
,
 必有
必有

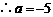 或
或
剖析:由于忽视集合中元素应互异这一特征,产生增解的错误.求出 的值后,还必须检验是否满足集合中元素应互异这一特征.
的值后,还必须检验是否满足集合中元素应互异这一特征.
事实上,(1)当 时,
时,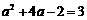 ,
,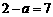 不满足
不满足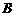 中元素应互异这一特征,故
中元素应互异这一特征,故 应舍去.
应舍去.
(2)当 时,
时,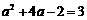 ,
,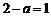 满足
满足 且集合
且集合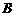 中元素互异.
中元素互异.
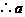 的值为1.
的值为1.
例2 已知 ,
, ,若
,若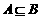 ,则
,则 的值为 .
的值为 .
错解: 由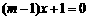 得
得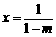
由 得
得 或
或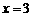

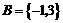

 或3
或3
 或
或
剖析:由于忽视空集的特殊性――空集是任何集合的子集,产生丢解的错误,以上只讨论了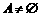 的情形,还应讨论
的情形,还应讨论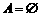 的情形,当
的情形,当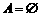 时,
时,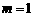 .
.
 的值为
的值为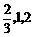 .
.
例1 集合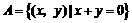 ,
, ,则
,则 .
.
错解: 解方程组 得
得

剖析: 产生错误的原因在于没有弄清楚集合中元素的形式,混淆点集与数集.集合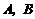 中的元素都是有序数对,即平面直角坐标系中的点,而不是数,因而
中的元素都是有序数对,即平面直角坐标系中的点,而不是数,因而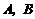 是点集,而不是数集.
是点集,而不是数集.
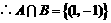
例7、已知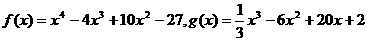 ,
,
A=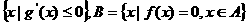 ,则B中的元素个数为
,则B中的元素个数为
A.有3个 B.有2个 C.有且仅有1个 D.不存在
解:由导数的知识可知:A={x|x2-12x+20≤0}={x|2≤x≤10},
又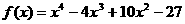 ,
,
∴
当x∈A时,易知: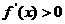 ∴f(x)在区间[2,10]上为增函数
∴f(x)在区间[2,10]上为增函数
而可求得f(2)<0,f(10)>0, ∴方程f(x)=0在区间[2,10]上有且仅有一解。
即集合B中仅有一个元素。
练习:
(1)
已知 ,
, 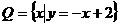 , 求
, 求
(2)
已知 ,
, 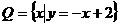 , 求
, 求
(3)
已知 ,
,  , 求B
, 求B
(4)已知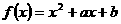 ,
, ,求M
,求M
例6、已知集合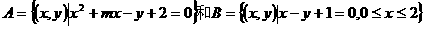 ,如果
,如果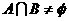 ,求实数a的取值范围。
,求实数a的取值范围。
剖析:从代表元素(x,y)看,这两个集合均为点集,又x2+mx-y+2=0及x-y+1=0是两个方程,故A∩B≠φ的实质为两个曲线有交点的问题,我们将其译成数学语言即为:“抛物线x2+mx-y+2=0与线段x-y+1=0(0≤x≤2)有公共点,求实数m的取值范围。”
解:由 ,得
,得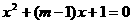 ①
①
 ,
, 方程①在区间[0,2]上至少有一个实数解.
方程①在区间[0,2]上至少有一个实数解.
首先,由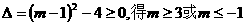 .
.
当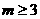 时,由x1+x2=-(m-1)<0及x1x2=1知,方程①只有负根,不符合要求;
时,由x1+x2=-(m-1)<0及x1x2=1知,方程①只有负根,不符合要求;
当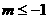 时,由x1+x2=-(m-1)>0及x1x2=1>0知, 方程①有两个互为倒数的正根,故必有一根在区间
时,由x1+x2=-(m-1)>0及x1x2=1>0知, 方程①有两个互为倒数的正根,故必有一根在区间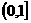 内,从而方程①至少有一个根在区间[0,2]内。
内,从而方程①至少有一个根在区间[0,2]内。
综上,所求m的取值范围是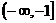 。
。
例7、已知集合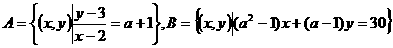 ,若
,若 ,求实数a的值。
,求实数a的值。
解:(1)当a=1时,集合B=Φ,符合题意。
(2)当a≠1时,易知A、B两集合均为点集,其中A集合为直线y=(a+1)(x-2)+3(x≠2)上的点集,B集合为直线上的点集,由 ,知两直线无公共点,故又有以下两种情况:
,知两直线无公共点,故又有以下两种情况:
①若两直线平行,则-(a+1)=a+1 ∴a=-1
②若直线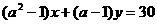 经过点(2,3),则
经过点(2,3),则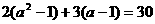 ,解之得:
,解之得: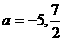 。
。
综上: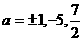
例5、已知集合A={a|ax2+4x-1≥-2x2-a恒成立},B={x| x2-(2m+1)x+m(m+1)<0},
若A∩B≠Φ,求实数m的取值范围。
分析:集合A是使不等式ax2+4x-1≥-2x2-a恒成立的a的取值范围,集合B是不等式x2-(2m+1)x+m(m+1)<0的解集,下面即可用相关知识解决。
解:由不等式ax2+4x-1≥-2x2-a恒成立,可得:(a+2)x2+4x+(a-1)≥0(★),
(1)当a+2=0时,即a=-2时,(★)式可化为x>3/4,显然不符合题意。
(2) 当a+2≠0时,欲使(★)式对任意x均成立,必需满足
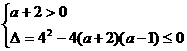 ,解之得A=
,解之得A=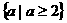 。
。
又可求得B={x|m<x<m+1},结合数轴,可得:m>1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com