
题目列表(包括答案和解析)
3、利用两平行平面的距离确定
对上例,有如下的计算方法:
解: 把平面EFG补成一个正四棱柱的截面所在的平面.则面GMT是正四棱柱ABCD-A1B1C1D1经过F、E、G的截面所在的平面.MG交BB1于N,TG交DD1于Q.作BP//MG,交CG于P,连结DP.则有平面GTM//平面PDB。它们之间的距离就是所求之距离,于是可以把点B平移到平面PDB上任何一个位置。
而这两个平行平面的距离d又同三棱柱GQN-PDB的体积有关,所以可以利用三棱柱的体积确定所求之距离。则有三棱柱GQN-PDB的体积V的关系式:

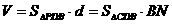 (
( ).易求出BN=
).易求出BN=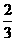 ,CP=
,CP= ,PB=PD=
,PB=PD=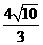 ,BD=
,BD= ,
, ,
,
由关系式( )可得,
)可得,
于是平行平面间的距离  ,即点B到面EFG的距离为
,即点B到面EFG的距离为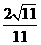 。
。
[点评]若两平面平行,则平面内的任一条直线到另一个平面的距离等于两平面间的距离,对于分别位于两个平行平面内的异面直线之间的距离也等于两平面间的距离。在解题过程中要注意体会。
2、 运用面面角或利用斜线和平面所成的角
例6、在直角梯形ABCD中, ,
, 。将
。将 沿AC折起使D到
沿AC折起使D到 ,如果二面角
,如果二面角
 为
为 ,求点
,求点 到面ABC的距离。
到面ABC的距离。
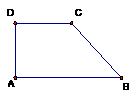

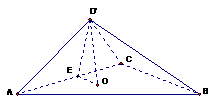
解:设 在平面ABC内的射影为O, E为AC的中点,连结OE
在平面ABC内的射影为O, E为AC的中点,连结OE
由于 ,故
,故 为二面角的平面角,即
为二面角的平面角,即 =
= 。又
。又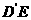 =
= ,所以
,所以 =
=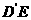
 =
=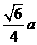 。
。
例7、已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于ABCD所在平面,且GC=2,求点B到平面EFG的距离.
解:设M为FE与CB的延长线的交点,作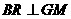 ,R为垂足. 又
,R为垂足. 又 ,
,
 所以平面BER⊥平面EFG。又ER为它们的交线
所以平面BER⊥平面EFG。又ER为它们的交线
∴∠REB就是EB与平面EFG所成的角θ
由△MRB∽△MCG,可得
 ,
,
在Rt△REB中, 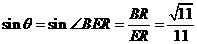
于是得所求之距离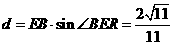 .
.
[点评]此法体现着角与距离间的转化,另一个变化是利用距离求角,应引起我们的足够重视。
1、等体积法(利用三棱锥的体积公式)
例5、已知在棱长为1的正方体 中,E、F分别是
中,E、F分别是 、CD的中点,求点B到平面
、CD的中点,求点B到平面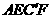 的距离。
的距离。
解:连结AE、BF、EF,则点B到平面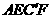 的距离即为点B到平面AEF的距离。设点B到平面AEF的距离为h, 根据
的距离即为点B到平面AEF的距离。设点B到平面AEF的距离为h, 根据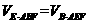 则
则
 ,得h=
,得h=
[点评] 由于四面体以不同面为底的体积相等,因而等体积法的关键是将距离看成是某四面体的高。
2、转移构造法
(1)利用平行线转换点
例2、在直三棱柱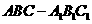 中,
中,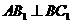 ,
, (b>a)
(b>a)
 (1)求证:
(1)求证: (2)求点
(2)求点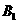 到平面
到平面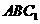 的距离.
的距离.
解:(1)连结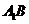 ,则
,则 ,又
,又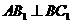 ,故
,故 。知
。知 ,得
,得 ,知
,知 。
。
(2)由(1)得 .
.


过 作
作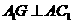 于G,
于G,  ,
, 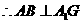
从而 . 故
. 故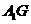 即为所求的距离。易求
即为所求的距离。易求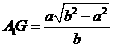 。
。
[点评]利用直线与平面平行,把所求的点到平面的距离转移到平行线上另一点到平面的距离来求,是我们常用的方法。
(2)对称转移或利用定比分点
 例3、如图,已知ABCD是矩形,AB=a,AD= b,PA^平面ABCD,PA=2c,Q是PA的中点.求P到平面BQD的距离.
例3、如图,已知ABCD是矩形,AB=a,AD= b,PA^平面ABCD,PA=2c,Q是PA的中点.求P到平面BQD的距离.
解:过A作 垂足为E,连结QE。∵平面BQD经过线段PA的中点,∴P到平面BQD的距离等于A到平面BQD的距离.在△AQE中,作AH^QE于H.∵BD^AE,BD^QE,∴BD^平面AQE.∴BD^AH,AH^平面BQE,即AH为A到平面BQD的距离.
垂足为E,连结QE。∵平面BQD经过线段PA的中点,∴P到平面BQD的距离等于A到平面BQD的距离.在△AQE中,作AH^QE于H.∵BD^AE,BD^QE,∴BD^平面AQE.∴BD^AH,AH^平面BQE,即AH为A到平面BQD的距离.
 在Rt△AQE中,∵AQ=c,AE=
在Rt△AQE中,∵AQ=c,AE=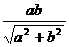 ,∴AH=
,∴AH= .
.
例4、已知正方体的棱长为1, 为上底面
为上底面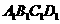 的中心。
的中心。
求点 到平面
到平面 的距离。
的距离。
析:点 到平面
到平面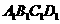 的距离为线段
的距离为线段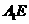 的长,易求得
的长,易求得 .又
.又 为
为 的中点,故点
的中点,故点 到平面
到平面 的距离为
的距离为 。
。
 [点评] 转移构造常利用已知平面点分某条斜线段所成的比,体现着转化的思想。
[点评] 转移构造常利用已知平面点分某条斜线段所成的比,体现着转化的思想。
转化到在某平面内,求出点和垂足间的线段的长。
1、 用定义直接构造法
 例1、如图,三棱锥S-ABC中,
例1、如图,三棱锥S-ABC中,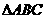 是等腰三角形,
是等腰三角形,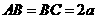 ,
, ,且
,且 面ABC,SA=3a。求点A到平面SBC的距离。
面ABC,SA=3a。求点A到平面SBC的距离。
解:作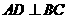 交BC于D,连结SD.
交BC于D,连结SD.
 平面ABC,根据三垂线定理有
平面ABC,根据三垂线定理有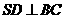
又 ,
,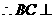 平面SAD。又
平面SAD。又 平面SBC,
平面SBC,
 平面SBC
平面SBC 平面ADS,且平面SBC
平面ADS,且平面SBC 平面ADS=SD
平面ADS=SD
 过点A作
过点A作 于H,则AH
于H,则AH 平面SBC。在
平面SBC。在 中,SA=3a,
中,SA=3a,
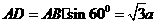 ,
,
故点A到平面SBC的距离为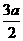 。
。
[点评]利用构造法关键是定位点在面内的射影。常常要寻找过已知点且与所给面垂直的面,再过已知点作两垂面交线的垂线。
5、解集错误地写成不等式或不注意用字母表示的两个数的大小:
例题5、若a<0,
则关于x的不等式 的解集是
.
的解集是
.
[错解]x<-a或x >5 a
[分析]把解集写成了不等式的形式;没搞清5 a和-a的大小.
[正解]{x|x<5 a或x >-a }
4、不理解有关逻辑语言:
例题4、“非空集合M的元素都是集合P的元素”是假命题,则以下四个命题:⑴M的元素都不是P的元素;⑵M中有不属于P元素;⑶M中有P的元素;⑷M的元素不都是P的元素,其中真命题的个数有……………………………………………………………( )
(A)1个 (B)2个 (C)3个 (D)4个
[错解]常见错误是认为第(4)个命题不对.
[分析]实际上,由“非空集合M的元素都是集合P的元素”是假命题知非空集合M不是集合P的子集,故“M的元素不都是P的元素”(M的元素有的是、有的不是集合P的元素,或M的元素都不是P的元素)是正确的.
[正解]正确答案是B(2、4两个命题正确).
3、搞不清楚是否能取得边界值:
例题3、A={x|x<-2或x>10},B={x|x<1-m或x>1+m}且B A,求m的范围.
A,求m的范围.
[错解]因为B A,所以:
A,所以: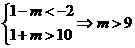 .
.
[分析]两个不等式中是否有等号,常常搞不清楚.
[正解]因为B A,所以:
A,所以: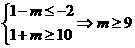 .
.
2、分不清四种集合: 、
、 、
、 、
、 的区别.
的区别.
例题2、已知函数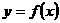 ,
, ,那么集合
,那么集合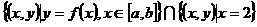 中元素的个数为…………………………………………………………………………(
)
中元素的个数为…………………………………………………………………………(
)
(A) 1 (B)0 (C)1或0 (D) 1或2
[错解]:不知题意,无从下手,蒙出答案D.
[分析]:集合的代表元,决定集合的意义,这是集合语言的特征.事实上, 、
、 、
、 、
、 分别表示函数
分别表示函数 定义域,值域,图象上的点的坐标,和不等式
定义域,值域,图象上的点的坐标,和不等式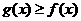 的解集.
的解集.
[正解]:本题中集合的含义是两个图象的交点的个数.从函数值的唯一性可知,两个集合的交中至多有一个交点.即本题选C.
1、忽略 的存在:
的存在:
例题1、已知A={x|
 },B={x|
},B={x|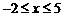
 },若A
},若A B,求实数m的取值范围.
B,求实数m的取值范围.
[错解]A B
B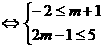 ,解得:
,解得: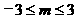
[分析]忽略A= 的情况.
的情况.
[正解](1)A≠ 时,A
时,A B
B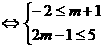 ,解得:
,解得: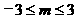 ;
;
(2)A= 时,
时,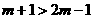 ,得
,得 .
.
综上所述, m的取值范围是(
m的取值范围是(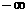 ,
,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com