
题目列表(包括答案和解析)
2.用数形结合的思想解集合问题。
例8、求集合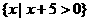 与集合
与集合 有公共元素的
有公共元素的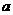 的取值范围。
的取值范围。
解析:集合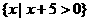 即为不等式
即为不等式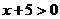 的解集,是大于
的解集,是大于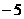 的所有实数;集合
的所有实数;集合 即为不等式
即为不等式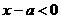 的解集,是小于
的解集,是小于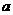 的所有实数,在数轴上表示出两个集合,
的所有实数,在数轴上表示出两个集合,

可见,若要两个集合有公共部分,必须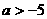 。
。
答案: 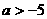 。
。
1.集合与方程。
例7、若方程 的解集是
的解集是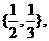 求
求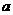 .
. 的值。
的值。
解析:由解集是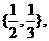 可知这是个二次方程,即
可知这是个二次方程,即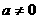 ,
,
由韦达定理,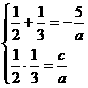 ,解得
,解得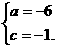
答案: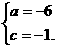
8. 回到定义,也是一法
在遇到难入手的题目时,有时回到定义上来,反而变简单了。
例8. 设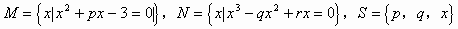 ,且
,且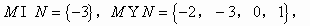 则S为( )
则S为( )
A. 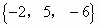
B. 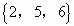
C. 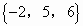
D. 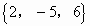
分析:由题意,可求出集合M和N,从而求出p,q,r。
由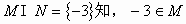
故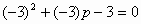
解得
由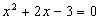
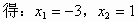
故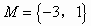
又由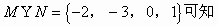
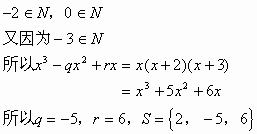
故选(D)。
7. 注意隐含条件
例7. 全集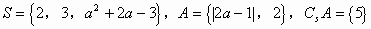 ,求实数a的值。
,求实数a的值。
错解:因为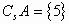
所以
从而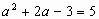
解得:
分析:导致错误的原因是没有考虑到隐含条件,因为S是全集,所以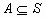 。
。
当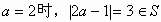 ,符合题意;
,符合题意;
当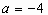 时,
时,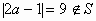 ,不符合题意,故
,不符合题意,故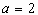 。
。
注:在解有关含参数的集合题时,需要进行验证结果是否满足题中的条件(包含隐含条件)。
6. 注意分类讨论的重要性
例6. 已知集合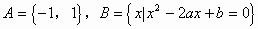 ,若
,若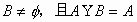 ,求实数a和b的值。
,求实数a和b的值。
分析:因为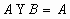 ,故
,故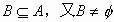 ,故B中含一个或两个元素,通过讨论,可求出:
,故B中含一个或两个元素,通过讨论,可求出:
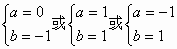
5. 注意取等的可能性
例5. 已知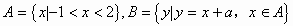 ,
,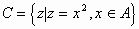 ,且
,且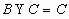 ,求实数a的取值范围。
,求实数a的取值范围。
分析:由已知得:

注:不要忽略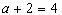 的情况。
的情况。
4. 注意字母的取值范围
当参数包含于多个元素的表达式时,运算过程中容易扩大参数的取值范围,应注意检验,否则会发生错解。
例4. 已知集合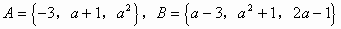 ,且
,且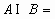
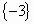 ,求实数a的值。
,求实数a的值。
错解:由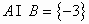 ,知
,知

分析:当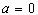 时,
时,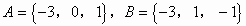
此时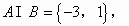

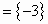 矛盾,应舍去。
矛盾,应舍去。
3. 注意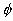 的特殊性
的特殊性
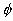 是任何集合的子集,是任何非空集合的真子集,与任何集合的并集等于集合本身,忽视它的特殊性,同样会造成解题错误。
是任何集合的子集,是任何非空集合的真子集,与任何集合的并集等于集合本身,忽视它的特殊性,同样会造成解题错误。
例3. 已知集合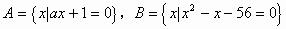 ,若
,若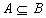 ,求由实数a组成的集合C。
,求由实数a组成的集合C。
错解:因为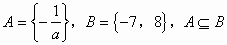
所以
即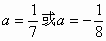
所以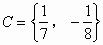
分析:导致错误的原因是漏掉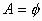 的情形,当
的情形,当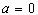 时,
时,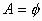 亦满足条件,可得:
亦满足条件,可得:
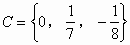
2. 注意集合元素的含义
集合中元素是有一定意义的,对此,稍有疏忽就会导致解题失误。
例2. 设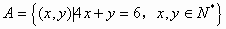 ,
,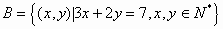 ,则
,则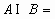 ___________。
___________。
错解:由方程组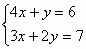
解得: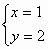
故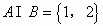
分析:导致错误的原因是没有正确理解集合元素的含义,A、B中的元素是有序数对,即表示平面直角坐标系中的点,故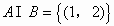
1. 注意集合中元素的互异性
集合中任何两个元素都是不同的,相同元素归入同一集合时只能算作一个元素,因此集合中元素是没有重复的,忽视互异性会引出错解。
例1. 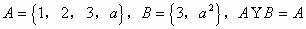 ,求实数a的值。
,求实数a的值。
错解:由题意知:
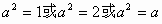
即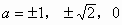
分析: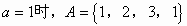 ,这与集合元素的互异性相矛盾,舍去
,这与集合元素的互异性相矛盾,舍去 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com