
题目列表(包括答案和解析)
3.通过对立方体及空间图形的研究挖究高考解答题的模式.
高考解答题往往是要解决两大问题:一是证明题,二是计算题.处理方式有两种:⑴在证明中要以典型的三段论的形式,严格按照演绎推理的步骤完成推理的论证;计算时并非单纯的数字计算,而是与作图与证明相结合的,立体几何计算题的主要步骤可归纳为:“画-证-算”三步.“画”是画图,添加必要的辅助线,或画出所要求的几何量,或进行必要的转换化,“证”是证明,证明所画的几何量即为所求,然后进行最后一步计算.这三步之间紧密相连,环环相扣,相互制约,是解决立体几何题的思维程序.⑵由垂直关系建立空间直角坐标系,运用向量处理即可.
2.加强立方体与其它内容的渗透的研究:立方体与排列组合的结合,象染色问题,计数问题;立方体与解析几何的结合,象轨迹问题;立方体与函数方程的结合,象最值问题;立方体与代数三角的结合,象角度距离问题;立方体与其它学科的结合,象化学晶体问题等.这样有助于对正方体的深刻认识与实际应用.
1.加强对立方体的研究,对空间图形的研究以培养学生的空间想象能力,数形转换能力与逻辑思维能力.
⑴对立方体本身的研究:如:立方体的内切球,外接球,球与立方体的棱相切等;立方体与正四面体的联系;以正方体各面的中点为顶点可构成正八面体等.
⑵对空间图形问题中解题方法的研究:以立方体为载体的方法有:平移求角法,割体补形法,面积射影法,体积相等法,侧面展形法,转化化归法,空间向量法等.
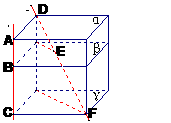 ⑶构造立方体以解决有关问题(第二册下B
⑶构造立方体以解决有关问题(第二册下B  3)“已知三个平行平面α、β、γ与两条直线
3)“已知三个平行平面α、β、γ与两条直线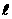 、
、 分别相交于点A、B、C和点D、E、F(图1),求证:
分别相交于点A、B、C和点D、E、F(图1),求证: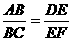 .”解答此题时学生很容易误将
.”解答此题时学生很容易误将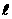 与
与 共面去理解造成错误.其实构造正方体(图2)可加强直观性以帮助学生理解.
共面去理解造成错误.其实构造正方体(图2)可加强直观性以帮助学生理解.
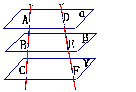
图1 图2
通过对立方体及空间图形的研究可培养学生的认识空间图形的能力,建立起空间概念,准确地理解并熟练运用概念、性质、公理、定理进行判断、推理与转化(如:①线线、线面、面面垂直关系的转化及平行关系的转化,②把空间距离和角向平面距和平面角的转化,③文字语言、符号语言、图形语言三者的相互转化.)等
8.2004年湖北(18)如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱BC的中点,点F 是棱CD上的动点.试确定点F的
使得D1E⊥平面AB1F.
 分析:以A为坐标标原点,建立如图所未的空间直角坐标系.
分析:以A为坐标标原点,建立如图所未的空间直角坐标系.
运用方程思想(借助向量的数量积)求解.
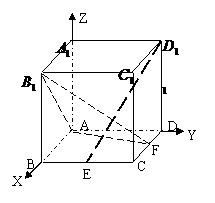 设DF=
设DF=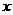 ,则A(0,0,0),B1(1,0,1),
,则A(0,0,0),B1(1,0,1),
D1(0,1,1),E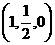 ,F(
,F(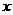 ,1,0)
,1,0)
∴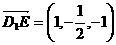 ,
, 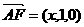 .
.
于是D1E⊥平面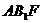 ∴
∴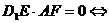
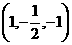 .
.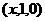 =0
=0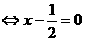
既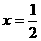 .故当点F是CD的中点时,D1E⊥平面AB1F.
.故当点F是CD的中点时,D1E⊥平面AB1F.
在近几年的高考试题中,立方体不仅包涵了所有的数学思想方法,密切了与中学数学中其它内容的联系,更体现着从静到动,从单一到多方面,从立方体本身应用问题到利用立方体去解决问题的发展变化.仔细研究这些变化对学好空间几何无疑是有裨益的.
几点思考:
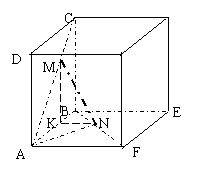
7. 2002全国卷(18) 如图,正方形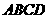 、
、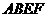 的边长都是1,而且平面
的边长都是1,而且平面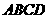 、
、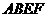 互相垂直.点
互相垂直.点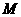 在
在 上移动,点
上移动,点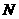 在
在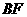 上移动,
上移动,
若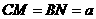
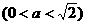 .
.
(1)求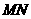 的长;
的长;
(2)当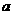 为何值时,
为何值时,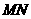 的长最小;
的长最小;
分析:将图形补成为正方体(如图)运用函数思想求解.
(1)作MK⊥AB于K,连KN.由面ABCD⊥面ABEF
得MK⊥KN.从而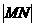 =
=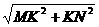 ……①
……①
 又由
又由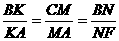 得KN∥AF.
得KN∥AF.
从而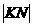 =
=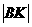 =
=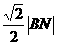 =
= ……②
……②
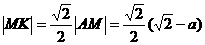 ……③
……③
将②③代入①有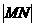 =
= =
=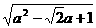 为所求.
为所求.
(2)运用函数配方法,由(Ⅰ)知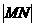 =
=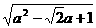 .
. 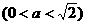 .
.
配方有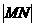 =
=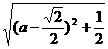 ≥
≥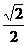
即当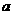 =
=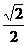 时,
时,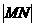 取最小值
取最小值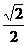 .
.
注:对空间图形中含有一些“动态”因素(象距离、角度等)的问题,可考虑能否把这一动源作为自变量,构造目标函数,用函数的思想来处理.
6.2004年湖南卷(10) 从正方体的八个顶点中任取三个点为顶点作三角形,其中直角三角形的个数为
(A)56 (B) 52 (C)48 (D)40
分析:可将合条件的直角三角形分为两类:
第一类:三个顶点在正方体的同一个面上时有:6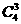 =24个.
=24个.
第二类:三个顶点在正方体的相对的两个面上时,直角三角形所在的平面一定是正方体的对角面,因而有:6×4=24个.
故共有:24+24=48个.从而选 (C)
注:以几何体为载体考查排列与组合的有关问题是高考的传统题型,要做到不重复不遗漏地分类并且注意几何体的结构特点去求解.
5.2000年全国卷(16)如图,E、F分别为正方体的面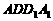 、
、
面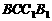 的中心,则四边形
的中心,则四边形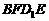 在该正方体的面上的射
在该正方体的面上的射
影可能是______。(要求:把可能的图的序号都填上)
分析:
 因正方体是由三对平行面所组成,所以只要将四边形
因正方体是由三对平行面所组成,所以只要将四边形 在三个方向上作投影即可,因而可分为三类情况讨论.
在三个方向上作投影即可,因而可分为三类情况讨论.
⑴在面ABCD上作投影可得②(平行四边形).
⑵在面 上作投影可得③(线段).
上作投影可得③(线段).
⑶在面 上作投影可得②(平行四边形).
上作投影可得②(平行四边形).
故可填为:②③
注:截面、射影的问题是空间图形和平面问题间变换的一种重要题型,象本题一样的定性分析题一定要抓住图形的特性(平行、垂直等)进行分析.
4.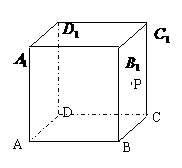 2004年北京卷(4)如图,在正方体ABCD-A1B1C1D1中,P是侧面BB1C1C内一动点,若P到直线BC与直线C1D1的距离相等,则动点P的轨迹所在的曲线是
2004年北京卷(4)如图,在正方体ABCD-A1B1C1D1中,P是侧面BB1C1C内一动点,若P到直线BC与直线C1D1的距离相等,则动点P的轨迹所在的曲线是
(A) 直线
(B) 圆
(C) 双曲线
(D) 抛物线
分析:易知P到直线C1D1的距离为: .
.
由C1是定点, BC是定直线.
条件即动点P到定点C1的距离等于到定直线BC的距离.符合抛物线的定义,化归为抛物线问题.故选(D)
注:立几中的解几问题是近年来才露脸的题型,要求熟练掌握立体几何和解析几何所有知识内容,更要有跳跃的思维,较强的转换能力.
3. 2003年全国(理)(16).下列5个正方体图形中,
2003年全国(理)(16).下列5个正方体图形中, 是正方体的一条对角线,点M、N、P分别为其所在棱的中点,能得出
是正方体的一条对角线,点M、N、P分别为其所在棱的中点,能得出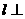 面MNP的图形的序号是
(写出所有符合要求的图形序号)__________.
面MNP的图形的序号是
(写出所有符合要求的图形序号)__________.
① ② ③ ④ ⑤
分析:易知①是合要求的,由于五个图形中的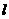 在同一位置,只要观察图②③④⑤ 中的平面MNP哪一个和①中的平面MNP平行(转化为面面平行) 即可.
在同一位置,只要观察图②③④⑤ 中的平面MNP哪一个和①中的平面MNP平行(转化为面面平行) 即可.
故为: ①④⑤
注:本题中选①中平面MNP作为“参照系”,可清淅解题思路,明确解题目标.
2.2003年全国卷(12)一个四面体的所有棱长都为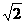 ,四个顶点在同一球面上,则此球的表面积为( )
,四个顶点在同一球面上,则此球的表面积为( )
(A)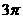 (B)4
(B)4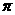 (C)
(C) (D)
(D)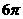
分析:本题中没有立方体,可充分挖掘是正四面体特点补形成立方体.
如图,将正四面体ABCD补成立方体,则正四面体、立方体的中心
与其外接球的球心共一点.因为正四面体的棱长为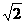 ,
,
所以正方体棱长为1,从而外接球半径R=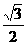 ,得
,得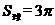 .故选(A).
.故选(A).
注:“补形割体”构造模型,进行适当的变形为熟悉的模型从而很方便地进行计算使问题得到顺利的解决,是处理空间图形中惯用的手段.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com