
题目列表(包括答案和解析)
5.在△ABC中, ,若使绕直线
,若使绕直线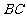 旋转一周,
旋转一周,
则所形成的几何体的体积是( )
A.  B.
B.  C.
C.  D.
D.
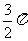
4.正方体的内切球和外接球的半径之比为( )
A.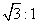 B.
B.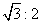 C.
C.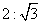 D.
D.
3.长方体的一个顶点上三条棱长分别是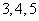 ,且它的
,且它的 个顶点都在
个顶点都在
同一球面上,则这个球的表面积是( )
A.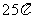 B.
B. C.
C. D.都不对
D.都不对
2.棱长都是 的三棱锥的表面积为( )
的三棱锥的表面积为( )
A. 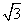 B.
B. 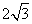 C.
C. 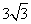 D.
D. 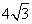
1.有一个几何体的三视图如下图所示,这个几何体应是一个( )
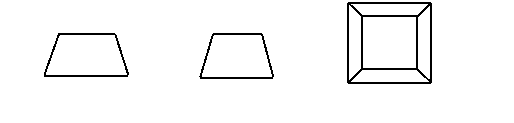 A.棱台 B.棱锥
C.棱柱 D.都不对
A.棱台 B.棱锥
C.棱柱 D.都不对

5、 抽象向具体转化
抽象向具体转化
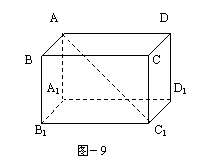 例7 A、B、C是球O面上三点,弧AB、AC、BC的度数分别是90°、90°、60°。求球O夹在二面角B-AO-C间部分的体积。
例7 A、B、C是球O面上三点,弧AB、AC、BC的度数分别是90°、90°、60°。求球O夹在二面角B-AO-C间部分的体积。
分析:此题难点在于空间想象,即较抽象。教师 引导学生读题:条件即∠AOB=∠AOC=90°,∠BOC=60°,然后给出图形(如图8),则可想象此题意即为用刀沿60°二面角,以直径为棱将一个西瓜切下一块,求这一块西瓜的体积,(答: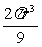 )。问题于是变得直观具体多了。
)。问题于是变得直观具体多了。
例8 三条直线两两垂直,现有一条直线与其中两条直线都成60°角,求此直线与另外一条直线所成的角。
分析:由条件想象到长方体的三条棱也两两垂直,于是问题可以转化为如下问题:长方体一条对角线与同一顶点上的三条棱所成的角分别是60°、60°、α,求α的大小。
根据长方体的性质,有cosα+cos60°+cos60°=1,可求得α=45°。
立体几何的教学,关键是要调动学生的学习兴趣,让他们学会联想与转化。立体几何的许多定理、结论源自生活实际,源自平面几何,要教会学生联想实际模型,联想平面几何中已经熟悉的东西,借助可取之材来建立空间想象,加强直观教学,这样就容易让学生接受,让他们喜欢上这一门学科,从而更有效地培养他们的空间想象力,提高他们解决立体几何问题的能力。
4、 等积转化
等积转化
“等积法”在初中平面几何中就已经有所应用,是一种很实用的数学方法与技巧。立体几何中的“等积转化”(或称等积变换)是以面积、体积(尤其是四面体的体积)作为媒介,来沟通有关元素之间的联系,从而使问题得到解决。
例6 如图7,已知ABCD-A1B1C1D1是棱长为a的正方体,E、F分别为棱AA1与CC1的中点,求四棱锥A1-EBFD1的体积。
略解:易证四边形EBFD1是菱形,
连结A1C1、EC1、AC1、AD1,
则VA1-EBFD1=2VA-EFD=2VF- A1ED1=2VC1- A1ED1
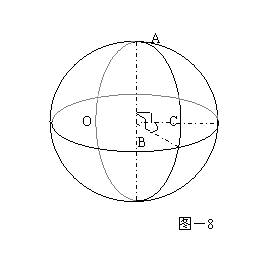 =2VE- A1C1D1=VA-A1C1D1=
=2VE- A1C1D1=VA-A1C1D1=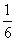 V正方体AC1=
V正方体AC1=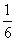 a3。
a3。
3、割补转化
“割形”与“补形”是解决立体几何问题的常用方法之一,通过“割”或“补”可化复杂图形为已熟知的简单几何体,从而较快地找到解决问题的突破口。
 例5 如图5,三棱锥P-ABC中,已知PA⊥BC,PA=BC=n,
例5 如图5,三棱锥P-ABC中,已知PA⊥BC,PA=BC=n,
PA与BC的公垂线ED=h,
求证:三棱锥P-ABC的体积V=n2h.
此题证法很多,下面用割补法证明如下:
分析一:如图5,连结AD、PD,∵BC⊥DE,BC⊥AB,
∴BC⊥平面APD,又DE⊥AP,
∴VP-ABC=VB-APD+VC-APD=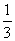 BC·S⊿APD=
BC·S⊿APD=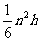 。
。
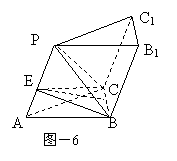 分析二:如图6,以三棱锥P-ABC的底面为底面,侧棱PA为侧棱,补成三棱拄 PB1C1-ABC,连结EC、EB,则易证AP⊥平面EBC,
分析二:如图6,以三棱锥P-ABC的底面为底面,侧棱PA为侧棱,补成三棱拄 PB1C1-ABC,连结EC、EB,则易证AP⊥平面EBC,
∴V三棱拄=AP·S⊿EBC= n2h。
n2h。
∴VP-ABC
=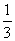 V三棱拄 =
V三棱拄 = 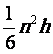 。
。
2、降维转化
 由三维空间向二维平面转化,是研究立体几何问题的重要数学方法之一。降维转化的目的是把空间的基本元素转化到某一个平面中去,用学生们比较熟悉的平面几何知识来解决问题。如线面垂直的判定定理的证明就是转化为三角形全等的平面问题。
由三维空间向二维平面转化,是研究立体几何问题的重要数学方法之一。降维转化的目的是把空间的基本元素转化到某一个平面中去,用学生们比较熟悉的平面几何知识来解决问题。如线面垂直的判定定理的证明就是转化为三角形全等的平面问题。
|
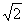 ,BB1=2,
,BB1=2, ,E、F分别为AA1、C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度为
.
,E、F分别为AA1、C1B1的中点,沿棱柱的表面从E到F两点的最短路径的长度为
. 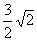
分析:这类问题通常都是将几何体的侧面展开成平面图形来解决。
又如异面直线所成的角、线面角、面面角的计算,最终都是转化为平面上两相交直线成的角来进行的。
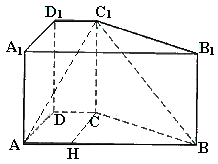 例4 如图-4直四棱柱
例4 如图-4直四棱柱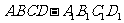 中,
中,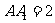 ,底面ABCD是直角梯形,∠A是直角,AB||CD,AB=4,AD=2,DC=1,求异面直线
,底面ABCD是直角梯形,∠A是直角,AB||CD,AB=4,AD=2,DC=1,求异面直线 与DC所成角的大小.(结果用反三角函数值表示)
与DC所成角的大小.(结果用反三角函数值表示)
解:由题意AB//CD,
 是异面直线BC1与DC所成的角.
是异面直线BC1与DC所成的角.
连结AC1与AC,在Rt△ADC中,可得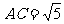 ,
,
又在Rt△ACC1中,可得AC1=3.
在梯形ABCD中,过C作CH//AD交AB于H,
|

又在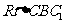 中,可得
中,可得 ,
,
在
∴异而直线BC1与DC所成角的大小为。
实现空间问题向平面问题转化的方法很多,常用的就有:平移法、射影法、展开法和辅助面法等等。
1、 位置关系的转化
线线、线面、面面平行与垂直的位置关系是立体几何中的一个重点内容,其精髓就是平行与垂直位置关系的相互依存及转化,平行与垂直问题不但能横向转化,而且可以纵向转化。
例1 已知三棱锥S-ABC中,∠ABC=90°,侧棱SA⊥底面ABC,点A在棱SB和SC上的射影分别是点E、F。求证EF⊥SC。
 分析:∵A、E、F三点不共线,AF⊥SC,
分析:∵A、E、F三点不共线,AF⊥SC,
∴要证EF⊥SC,只要证SC⊥平面AEF,
只要证SC⊥AE(如图1)。
又∵BC⊥AB,BC⊥SA,∴BC⊥平面SAB,
∴SB是SC在平面SAB上的射影。
∴只要证AE⊥SB(已知),∴EF⊥SC。
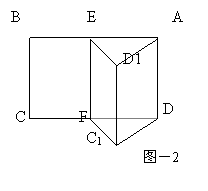 例2 设矩形ABCD,E、F分别为AB、CD的中点,以EF为棱将矩形
例2 设矩形ABCD,E、F分别为AB、CD的中点,以EF为棱将矩形
折成二面角A-EF-C1(如图-2)。求证:平面AB1E∥平面C1DF。
分析一(纵向转化):
∵AE∥DF,AE 平面C1DF,
平面C1DF,
∴ AE∥平面C1DF.同理,B1E∥平面C1DF,
又AE∩B1E=E,∴平面AB1E∥平面C1DF。
分析二(横向转化):
∵AE∥EF,B1E⊥EF,且AE∩B1E=E,∴EF⊥平面C1DF。
同理,EF⊥平面C1DF 。平面AB1E∥平面C1DF。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com