
题目列表(包括答案和解析)
1.化简[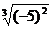 ]
] 的结果为(
)
的结果为(
)
A.5
B. C.-
C.- D.-5
D.-5
⒈根式的性质:⑴___________________________;⑵______________________________.
⒉指数运算法则⑴________________⑵________________⑶_________________.
⒊________________________________叫做指数函数,其定义域是_______,值域是__________________,单调性是__________________________________,图像的特征__________________________________.
⒈ D ⒉ B ⒊ C ⒋ A ⒌ A ⒍ A ⒎ y轴,x轴,y=x⒏ 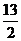 ⒐
⒐
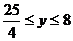
⒑解:依题意(a2-1)x2+(a+1)x+1>0对一切x∈R恒成立.当a2-1≠0时,其充要条件是: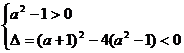 解得a<-1或a>
解得a<-1或a>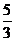 又a=-1,f(x)=0满足题意,a=1,不合题意.
又a=-1,f(x)=0满足题意,a=1,不合题意.
⒒解析:(1)定义域为(-∞,1),值域为(-∞,1)
(2)设1>x2>x1 ∵a>1,∴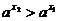 ,于是a-
,于是a-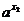 <a-
<a-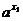 则loga(a-a
则loga(a-a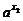 )<
)<
loga(a-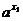 ) 即f(x2)<f(x1) ∴f(x)在定义域(-∞,1)上是减函数
) 即f(x2)<f(x1) ∴f(x)在定义域(-∞,1)上是减函数
(3)证明:令y=loga(a-ax) (x<1), 则a-ax=ay, x=loga(a-ay)
∴f-1(x)=loga(a-ax) (x<1)故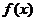 的反函数是其自身,
的反函数是其自身,
得函数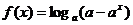 (x<1)图象关于y=x对称.
(x<1)图象关于y=x对称.
5.互为反函数,关于直线y=x对称.
2.⑴loga(MN)=logaM+logaN⑵loga(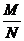 )=logaM-logaN⑶
)=logaM-logaN⑶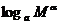 =αlogaM 3.
=αlogaM 3.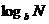 =
=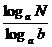 4.一般地,函数y=logax (a>0且a≠1,x>0);(0,+∞);
R;a>1时是增函数,0<a<1时是减函数;图像都在y轴右侧,都过(1,0).
4.一般地,函数y=logax (a>0且a≠1,x>0);(0,+∞);
R;a>1时是增函数,0<a<1时是减函数;图像都在y轴右侧,都过(1,0).
1.⑴0和负数没有对数,即N>0;⑵ loga1=0;⑶ logaa=1;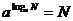
11.已知函数f (x)=loga(a-ax)且a>1, (1)求函数的定义域和值域;
(2)讨论f(x)在其定义域上的单调性;(3)证明函数图象关于y=x对称.
[答案]
10.已知函数f(x)=lg[(a2-1)x2+(a+1)x+1],若f(x)的定义域为R,求实数a的取值范围.
9.函数y =(log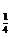 x)2-log
x)2-log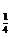 x2+5 在 2≤x≤4时的值域为_____
_
.
x2+5 在 2≤x≤4时的值域为_____
_
.
8.计算:log2.56.25+lg +ln
+ln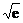 +
+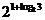 = .
= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com