
题目列表(包括答案和解析)
⒈ C ⒉ B ⒊ C ⒋ B ⒌ A ⒍ B ⒎ 第四,-6<x<-2 ⒏ R ⒐ 6
⒑解:由题意可设所求二次函数的解析式为 ,展开得
,展开得 ,
∴
,
∴ ,
,
∴ ,即
,即 ,解得
,解得 .
.
所以,该二次函数的图像是由 的图像向上平移 单位得到的,它的解析式是
的图像向上平移 单位得到的,它的解析式是 ,即
,即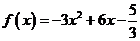 .
.
⒒解:函数 的表达式可化为
的表达式可化为 .
.
①当 ,即
,即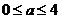 时,
时, 有最小值
有最小值 ,依题意应有
,依题意应有 ,解得
,解得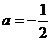 ,这个值与
,这个值与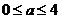 相矛盾.②当
相矛盾.②当 ,即
,即 时,
时,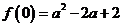 是最小值,依题意应有
是最小值,依题意应有 ,解得
,解得 ,又∵
,又∵ ,∴
,∴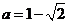 为所求.③当
为所求.③当 ,即
,即 时,
时, 是最小值,依题意应有
是最小值,依题意应有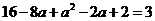 ,解得
,解得 ,又∵
,又∵ ,∴
,∴ 为所求.
为所求.
综上所述, 或
或 .
.
3.配方法;配凑法,换元法,待定系数法.
2.y=ax2+bx+c
(a≠0);y=a(x+ )2+
)2+ (a≠0);y=a(x-x1)(x-x2)(a≠0);R;a>0时[
(a≠0);y=a(x-x1)(x-x2)(a≠0);R;a>0时[ ,+∞),a<0时(-∞,
,+∞),a<0时(-∞,
 ];a>0时在
];a>0时在
(-∞, )上单调递减,在(
)上单调递减,在( ,+∞)上单调递增,a<0时在(-∞,
,+∞)上单调递增,a<0时在(-∞, )上单调递增,在(
)上单调递增,在( ,+∞)上单调递减;b=0时是偶函数,b≠0时是非奇非偶函数;一条抛物线,顶点(
,+∞)上单调递减;b=0时是偶函数,b≠0时是非奇非偶函数;一条抛物线,顶点( ,
, ),对称轴是直线x=
),对称轴是直线x= .
.
1.函数y=kx+b(k≠0);R;R;k>0时是增函数,k<0时是减函数;b=0时是奇函数,b≠0时是非奇非偶函数;一条直线;( ),(0,b).
),(0,b).
⒈一次函数y=(m-2)x+m2-3m-2,它的图像在y轴上的截距为-4,则实数m的值是( )
A.2或1 B.2 C.1 D.-2或1
⒉函数y=kx+k2-k过点(0,2),且是减函数,则k= ( )
A.-2 B.-1 C.-1,2 D.1,-2
⒊已知A(x1,3)和B(x2,3)是二次函数f(x)=ax2+bx+5上的两点
(x1≠x2),则f(x1+x2)=( )
A. B.5 C.3 D.2
B.5 C.3 D.2
⒋函数y=x2-3x-4的定义域为[0,m],值域为[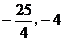 ],则m的取值范围是( )
],则m的取值范围是( )
A.(0,4] B.[ ] C.[
] C.[ ]
D.[
]
D.[ )
)
⒌若抛物线y=x2-6x+c的顶点在x轴上,则c的值为( )
A.9 B.19 C.3 D.0
⒍函数f(x)=2x2-mx+3,当x∈[-2,+∞)时是增函数,当x∈(-∞,-2]时是减函数,则f(1)=( )
A.-3 B.13 C.7 D.由m而定的其他常数
⒎函数y=3x+12的图像不经过______象限,若|y|<6,则x的取值范围___________________.
⒏函数y= 的定义域为____________________________________.
的定义域为____________________________________.
⒐若函数y=x2+(a+2)x+3,x∈[a,b]的图像关于直线x=1对称,则b为________________.
⒑若二次函数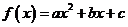 的图像与x轴有两个不同的交点
的图像与x轴有两个不同的交点 、
、 ,且
,且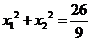 ,试问该二次函数的图像由
,试问该二次函数的图像由 的图像向上平移几个单位得到?
的图像向上平移几个单位得到?
⒒已知函数 在区间[0,2]上的最小值为3,求a的值.
在区间[0,2]上的最小值为3,求a的值.
[答案]
⒈________________________________叫做一次函数,其定义域是_____,值域是_______,单调性是___________________________,奇偶性是____________________,图像是________________,与坐标轴的交点是___________________.
⒉二次函数的解析式有________________________(一般式),____________________(顶点式),_____________________________(交点式),其定义域是______,值域是________
______________,单调性是__________________________________________________,奇偶性是____________________,图像是______________________________________.
⒊研究二次函数的主要方法是_______________________________,求函数解析式的常用方法有____________________________________________________.
⒈ B ⒉
B ⒊ A ⒋
A ⒌ A ⒍
A ⒎  ⒏
0<a<1
⒐ [
⒏
0<a<1
⒐ [ ]
]
⒑解:原式=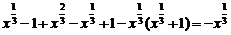
⒒解:设2x= t,∵0≤x≤2,∴1≤t≤4 原式化为:y=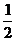 (t-a)2+1
(t-a)2+1
当a≤1时, ymin=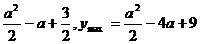 ;
;
当1<a≤ 时, ymin=1, ymax=
时, ymin=1, ymax= ;
;
当 <a<4时, ymin=1, ymax=
<a<4时, ymin=1, ymax=
当a≥4时, ymin=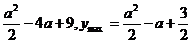 .
.
3.一般地,函数y=ax(a>0,a≠1,x∈R);R;(0,+∞);a>1时是增函数,
0<a<1时是减函数;函数图像在x轴上方且都通过点(0,1).
2.⑴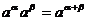 ⑵
⑵ ⑶
⑶
1.⑴ (n>1且n∈N+)⑵
(n>1且n∈N+)⑵ =
=
|a| , 当n为偶数时
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com