
题目列表(包括答案和解析)
7.设 ,
,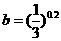 ,
, ,则
,则 ,
, ,
, 的大小关系是( )
的大小关系是( )
A. B.
B. C.
C. D.
D.
6.设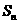 是等差数列
是等差数列 的前n项和,已知
的前n项和,已知 ,
, ,则
,则 等于( )
等于( )
A.13 B.35 C.49 D.63
5.下列说法错误的是( )
A.若集合A=﹛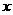 ︱
︱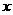 2+
2+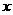
 0﹜,则-1
0﹜,则-1 A;
A;
B. 是
是 ,
, ,
, 成等比数列的充要条件;
成等比数列的充要条件;
C.命题“若m 0,则方程
0,则方程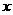 2+
2+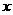 -m=0有实数根”的否命题是“若m
-m=0有实数根”的否命题是“若m 0,则方程
0,则方程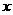 2+
2+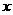 -m=0无实数根” ;
-m=0无实数根” ;
D.命题“若 =0,则
=0,则 =0”与命题“若
=0”与命题“若 ≠0,则
≠0,则 ≠0”都是真命题.
≠0”都是真命题.
4.已知 =
= (x
(x R且x≠-
R且x≠- )的反函数为
)的反函数为 ,则
,则 的值为( )
的值为( )
A. B.-
B.- C.
C. D.-1
D.-1
3.在等比数列 中,首项
中,首项 =
=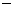 27,公比q=
27,公比q= ,则
,则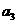 =( )
=( )
A. B.-3
C.3
D.
B.-3
C.3
D.
2.函数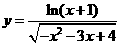 的定义域为( )
的定义域为( )
A. B.
B. C.
C. D.
D.
1.满足条件


 {0,1,2}的集合
{0,1,2}的集合 共有( )
共有( )
A.3个 B.6个 C.7个 D.8个
15、下列命题正确的有
(1) ,则
,则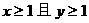 的否命题是假命题。
的否命题是假命题。
(2)函数 在定义域A内有反函数的充要条件是
在定义域A内有反函数的充要条件是 在定义域A内是单调函数。
在定义域A内是单调函数。
(3)若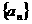 为等比数列,
为等比数列,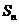 为其前
为其前 项和,则
项和,则 (
(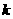 为奇数)也为等比数列。
为奇数)也为等比数列。
(4)函数 在定义域为
在定义域为 ,则函数
,则函数 在定义域为
在定义域为 。
。
三:解答题(共75分,解答应写出文字说明、证明过程或推演步骤。)
16(13分)、已知全集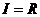 ,集合
,集合 ,集合
,集合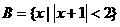 ,求集合
,求集合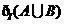 。
。
17(13分)、已知函数 是奇函数。
是奇函数。
(1):求 的值;
的值;
(2):当 时,求
时,求 的反函数
的反函数 。
。
18(13分)、已知函数 (
( ,且
,且 ),
), ,
,
 且
且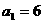 ,
,
(1)证明: 为等比数列
为等比数列
(2)求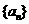 和
和 的通项公式。
的通项公式。
19(12分)、在2009年底的哥本哈根大会上,中国向全世界承诺,到2020年底,中国的炭排放将降至2009年炭排放量 的
的 ,目前我国的减排手段有两种,第一种是通过引进新技术,新工艺使得每年的炭排放比上一年炭排放总量均减少
,目前我国的减排手段有两种,第一种是通过引进新技术,新工艺使得每年的炭排放比上一年炭排放总量均减少 个百分点,第二种是通过教育与宣传使得全体国民具有节能减排的意识,进而减少炭排放。
个百分点,第二种是通过教育与宣传使得全体国民具有节能减排的意识,进而减少炭排放。
(1):若通过第二种方式的减排量每年均是一个常数 ,求2011年我国的炭排放量
,求2011年我国的炭排放量
(2):若全体国民齐心协力,使第二种方式的减排量能够占上年的炭排放总量的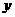 个百分点,要保证完成减排目标,求
个百分点,要保证完成减排目标,求 满足的范围。(已知
满足的范围。(已知 ,
,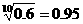 ,
,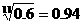 ,
, )
)
20(12分)、.设 为实数,函数
为实数,函数 .
.
(1)若 ,求
,求 的取值范围;
的取值范围;
(2)若 写出
写出 的单调递减区间;
的单调递减区间;
(3)设函数
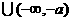 且
且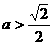 求不等式
求不等式 的解集.
的解集.
21(12分)、数列 的前
的前 项和记作
项和记作 ,满足
,满足 ,
, .
.
 求出数列
求出数列 的通项公式.
的通项公式.
(2) ,且
,且 对正整数
对正整数 恒成立,求
恒成立,求 的范围;
的范围;
(3)(原创)若 中存在一些项成等差数列,则称
中存在一些项成等差数列,则称 有等差子数列,若
有等差子数列,若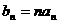 证明:
证明: 中不可能有等差子数列(已知
中不可能有等差子数列(已知 。
。
命题:梁 波 李长鸿
2010年重庆一中高2012级期末考试(本部)
14、已知数列 为单调增数列,则
为单调增数列,则 的范围为 。
的范围为 。
13、 的反函数的对称中心为
的反函数的对称中心为 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com