
题目列表(包括答案和解析)
19.解:⑴由
得 ,
,
又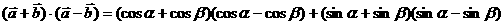

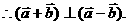
(2)
 同理
同理
由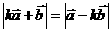 得
得
又 所以
所以 因
因 所以
所以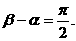
20(本小题满分14分) 已知
(Ⅰ)若 求
求 的表达式;
的表达式;
(Ⅱ)若函数f (x)和函数g(x)的图象关于原点对称,求函数g(x)的解析式;
(Ⅲ)若 在
在 上是增函数,求实数l的取值范围.
上是增函数,求实数l的取值范围.
19.(本题满分12分)已知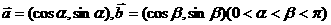 .
.
⑴求证: 互相垂直;
互相垂直;
⑵若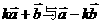 大小相等,求
大小相等,求 (其中k为非零实数).
(其中k为非零实数).
18. 

(2)f(x)=cos2x-4tcosx=2(cosx-t)2-1-2t2 (0≤cosx≤1)
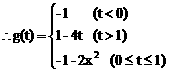
18. (本题满分12分)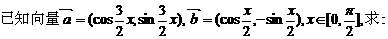

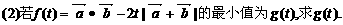
17.解:(1) ;
;
定义域:  ,值域:
,值域:
(2)T= ;单调递减区间:
;单调递减区间:
17. (本题满分12分)已知函数
(Ⅰ)求函数 的定义域,值域;
的定义域,值域;
(Ⅱ)求函数 的最小正周期和单调递减区间。
的最小正周期和单调递减区间。
16. 解: ∵e12=4, e22=1,
e1·e2=2×1×cos60°, ∴(2te1+7 e2)·(e1+ t e2)= 2t e12+(2t2+7)e1·e2+7t e22=2t2+15t+7.
……4分 ∴2t2+15t+7<0.
∴-7< t<- …….6分
…….6分
设2te1+7 e2=λ(e1+ t e2)(λ<0), 则2t=λ,且7= tλ, ∴2t2=7. ∴t =- ….8分,
….8分,
λ=-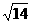 . ∴t =-
. ∴t =- 时, 2te1+7 e2与e1+ t e2的夹角为π……10分,
时, 2te1+7 e2与e1+ t e2的夹角为π……10分,
t的取值范围是(-7, - )∪(-
)∪(- , -
, - )….12分
)….12分
16.(12分)设两向量 ,
,  满足|
满足|  |=2, |e2|=1,
|=2, |e2|=1, 
 的夹角为60°, 若向量2t
的夹角为60°, 若向量2t +7
+7 与向量
与向量 + t
+ t  的夹角为钝角, 求实数t的取值范围.
的夹角为钝角, 求实数t的取值范围.
15.下面有四个命题:
(1)函数y=sin( x+
x+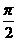 )是偶函数;(2)函数f (x)=|cos2x|的最小正周期是p;
)是偶函数;(2)函数f (x)=|cos2x|的最小正周期是p;
(3)函数f (x)=sin(x+ )在
)在 上是增函数;
上是增函数;
(4)函数f (x)=asinx-bcosx的图象的一条对称轴为直线x= ,则a+b=0.
,则a+b=0.
其中正确命题的序号是_(1)(4)____________________.
14. 发电厂发出的电是三相交流电,它的三根导线上的电流强度 I分别是时间t的函数I
则 0
.
0
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com