
题目列表(包括答案和解析)
19.已知圆 ,直线
,直线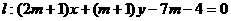 .
.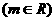
(1)证明不论 取何值,直线
取何值,直线 与圆恒交于两点;k+s-5#u
与圆恒交于两点;k+s-5#u 
(2)求直线被圆截得的弦长最短时的方程和最短弦长.
证明:直线方程为
解方程组 ,得
,得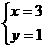 ,即直线恒过定点A(3,1)
,即直线恒过定点A(3,1)
 ,点A在圆C内,从而直线与圆恒交于两点
,点A在圆C内,从而直线与圆恒交于两点
(2)当弦长最短时,直线 ,又
,又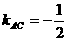 k+s-5#u
k+s-5#u 
此时直线 的方程为
的方程为 ,此时弦长为
,此时弦长为
18.(本小题满分12分)
如图,在正方体ABCD-A1B1C1D1中,E、F、G为棱AD、AB、A1A的中点.
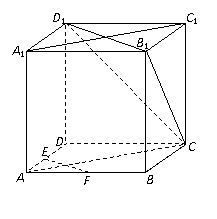 (1)求证:平面EFG∥平面CB1D1;
(1)求证:平面EFG∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1;
(3)求异面直线FG、B1C所成的角。
|
 在长方体
在长方体 中,对角线
中,对角线 .
.
又 E、F为棱AD、AB的中点,
E、F为棱AD、AB的中点,
 .
.  .
.
同理可证:GE// B1C ,EF∩GE=E
k+s-5#u 
 面EFG∥平面CB1D1.
面EFG∥平面CB1D1.
(2) 在长方体
在长方体 中,AA1⊥平面A1B1C1D1,而B1D1平面A1B1C1D1,
中,AA1⊥平面A1B1C1D1,而B1D1平面A1B1C1D1,
 AA1⊥B1D1.
AA1⊥B1D1.
又 在正方形A1B1C1D1中,A1C1⊥B1D1,
在正方形A1B1C1D1中,A1C1⊥B1D1, B1D1⊥平面CAA1C1.
B1D1⊥平面CAA1C1.
又 B1D1平面CB1D1,
B1D1平面CB1D1, 平面CAA1C1⊥平面CB1D1.
平面CAA1C1⊥平面CB1D1.
(3) 由(1)知GE// B1C,异面直线FG、B1C所成的角为600
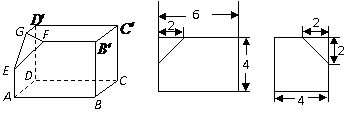
17.如下的三个图中,分别是一个长方体截去一个角所得多面体的直观图以及它的主视图和左视图(单位:cm)
(1)按照画三视图的要求画出该多面体的俯视图;
(2)按照给出的尺寸,求该多面体的体积;k+s-5#u 
(3)在所给直观图中连结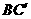 ,证明:
,证明: 面
面 .
.
解:(1)如图

 3分
3分
 (2)所求多面体体积
(2)所求多面体体积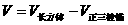
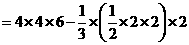
 .7分
.7分
(3)证明:在长方体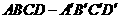 中,
中,
连结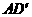 ,则
,则 .
.
因为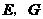 分别为
分别为 ,
,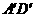 中点,所以
中点,所以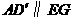
从而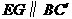 .又
.又 平面
平面 ,
,
所以 面
面 . --------------10分k+s-5#u
. --------------10分k+s-5#u 
13.5; 14. 0<a< 15. 16.
16. 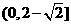
22.(本小题满分12分)
已知圆O: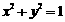 和定点A(2,1),由圆O外一点
和定点A(2,1),由圆O外一点 向圆O引切线PQ,切点为Q,且满足
向圆O引切线PQ,切点为Q,且满足 .
.
 (1) 求实数a、b间满足的等量关系;k+s-5#u
(1) 求实数a、b间满足的等量关系;k+s-5#u 
(2) 求线段PQ长的最小值;
(3) 若以P为圆心所作的圆P与圆O有公共点,试求半径取最小值时圆P的方程.
玉溪一中2009-2010学年上学期期末考试
高一年级数学试题
21.(本小题满分12分)已知函数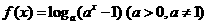 .
.
(1)求函数 的定义域;
的定义域;
(2)讨论函数 的单调性. k+s-5#u
的单调性. k+s-5#u 
20.(本小题满分12分)为了绿化城市,准备在如图所示的区域内修建一个矩形PQRC的草坪,且PQ∥BC,RQ⊥BC,另外△AEF的内部有一文物保护区.AB=100m,BC=80m,AE=30m,AF=20m.
(1) 求直线EF的方程.k+s-5#u 
(2) 应如何设计才能使草坪的占地面积最大?


19.(本小题满分12分)已知圆 ,直线
,直线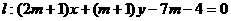 .
.
(1)证明不论 取何值,直线
取何值,直线 与圆恒交于两点;k+s-5#u
与圆恒交于两点;k+s-5#u 
(2)求直线被圆截得的弦长最短时的方程和最短弦长.
18.(本小题满分12分)如图,在正方体ABCD-A1B1C1D1中,E、F、G为棱AD、AB、A1A的中点.
(1)求证:平面EFG∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1 k+s-5#u  ;
;
|

17.(本小题满分10分)如下的三个图中,分别是一个长方体截去一个角所得多面体的直观图以及它的主视图和左视图(单位:cm)
(1)按照画三视图的要求画出该多面体的俯视图;k+s-5#u 
(2)按照给出的尺寸,求该多面体的体积;k+s-5#u 
(3)在所给直观图中连结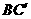 ,证明:
,证明: 面
面 .
.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com