3.1　 函数与方程

5．经市场调查分析知，某地明年从年初开始的前个月，对某种商品需求总量 (万件)近似地满足关系．

(1)写出明年第个月这种商品需求量 (万件)与月份的函数关系式，并求出哪几个月的需求量超过1．4万件；

(2)若计划每月该商品的市场投放量都是万件，并且要保证每月都满足市场需求，则至少为多少万件?

4．某厂每天需要本厂甲车间生产的某种零件10件，已知甲车间每天的生产能力为50件，生产准备费用为2500元／次，其它费用为200元／件，每件一年的库存费为365元．试问，一年中安排生产多少次时全年费用最少?(一年按365天计算)

3．一工厂对某种原料的全年需求量是Q吨，为保证生产又节省开支，打算全年分若干次等量订购，且每次用完后立即购进．已知每次订购费用是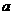元，工厂每天使用的原料数量相同，仓库贮存原料的年保管费用是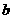元／吨，问全年订购多少次，才能使订购费用与保管费用之和最少?

2．如图，今有网球从斜坡O点处抛出路线方程是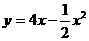；斜坡的方程为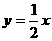，其中y是垂直高度(米)，是与O的水平距离(米)．

(1)网球落地时撞击斜坡的落点为A，写出A点的垂直高度，以及A点与O点的水平距离；

(2)在图象上，标出网球所能达到的最高点B，求OB与水平线O之间的夹角的正切值．

1．如图，河流航线AC段长40公里，工厂上；位于码头C正北30公里处，原来工厂B所需原料需由码头A装船沿水路到码头C后，再改陆路运到工厂B，由于水运太长，运费太高，工厂B与航运局协商在AC段上另建一码头D，并由码头D到工厂B修一条新公路，原料改为按由A到D再到B的路线运输．设=公里(0≤≤40)，每10吨货物总运费为y元，已知每10吨货物每公里运费，水路为l元，公路为2元．

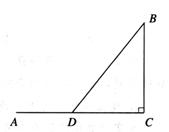
(1)写出y关于的函数关系式；

(2)要使运费最省，码头D应建在何处?

3.2　 函数模型及其应用

20.已知函数

(1)求函数的定义域；

(2)判断函数的奇偶性，并证明.

(3)讨论函数在定义域上的单调性如何？并思考函数f(x)的图象上是否存在两个不同的点A,B,使直线AB恰好与y轴垂直,若存在,求出A,B两点的坐标；若不存在,说明理由并加以证明.

19.已知正四棱锥R-ABCD的底面边长为4，高为6，点O是底面ABCD的中心，点P是RO的中点，点Q是△RBC的重心.　　　　　　　　　　　　

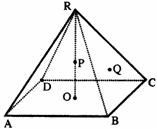(1)求证：面ROQ⊥面RBC；

(2)求直线PQ与底面ABCD所成的角；　　　　　　　　　　　　　　　　　　

(3)求异面直线PQ与BR所成的角的余弦值.

18.如图,四棱锥P-ABCD的底面是AB=2,BC=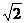的矩形,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD.

(Ⅰ)证明:BC⊥侧面PAB;

(Ⅱ)证明:侧面PAD⊥侧面PAB;

(Ⅲ)求侧棱PC与底面ABCD所成角的大小.