
题目列表(包括答案和解析)
3.已知圆x2+y2+2x-6y+F=0与x+2y-5=0交于A, B两点, O为坐标原点,
若OA⊥OB, 则F的值为 ( )
A 0 B 1 C -1 D 2
2.已知两点M(-2,0),N(2,0),点P满足 =12,则点P的轨迹方程为( )
=12,则点P的轨迹方程为( )
A. B.
B.
C. D.
D.
1.已知θ∈R,则直线 的倾斜角的取值范围是
( )
的倾斜角的取值范围是
( )
A.[0°,30°] B.
C.[0°,30°]∪ D.[30°,150°]
D.[30°,150°]
2.2《直线、平面平行的判定及其性质》测试
第1题. 已知 ,
, ,
,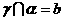 ,且
,且 ,求证:
,求证: .
.
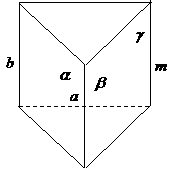
答案:证明:
 .
.
第2题. 已知: ,
, ,
,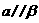 ,则
,则 与
与 的位置关系是( )
的位置关系是( )
A. B.
B.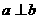
C. ,
, 相交但不垂直 D.
相交但不垂直 D. ,
, 异面
异面
答案:A.
第3题. 如图,已知点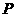 是平行四边形
是平行四边形 所在平面外的一点,
所在平面外的一点,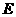 ,
, 分别是
分别是 ,
, 上的点且
上的点且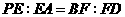 ,求证:
,求证: 平面
平面 .
.

答案:证明:连结 并延长交
并延长交 于
于 .连结
.连结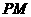 ,
,
 ,
, ,又由已知
,又由已知 ,
, .
.
由平面几何知识可得
 ,又
,又 ,
, 平面
平面 ,
,

 平面
平面 .
.
第4题. 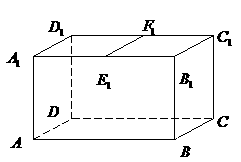 如图,长方体
如图,长方体 中,
中, 是平面
是平面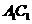 上的线段,求证:
上的线段,求证: 平面
平面 .
.
答案:证明:如图,分别在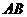 和
和 上截取
上截取 ,
, ,连接
,连接 ,
, ,
,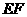 .
.
 长方体
长方体 的各个面为矩形,
的各个面为矩形,
 平行且等于
平行且等于 ,
, 平行且等于
平行且等于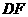 ,
,
故四边形 ,
, 为平行四边形.
为平行四边形.
 平行且等于
平行且等于 ,
, 平行且等于
平行且等于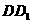 .
.
 平行且等于
平行且等于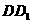 ,
, 平行且等于
平行且等于 ,
,
四边形 为平行四边形,
为平行四边形,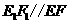 .
.
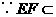 平面
平面 ,
, 平面
平面 ,
,


 平面
平面 .
.
第5题. 如图,在正方形 中,
中,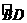 的圆心是
的圆心是 ,半径为
,半径为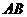 ,
, 是正方形
是正方形 的对角线,正方形以
的对角线,正方形以 所在直线为轴旋转一周.则图中Ⅰ,Ⅱ,Ⅲ三部分旋转所得几何体的体积之比为 .
所在直线为轴旋转一周.则图中Ⅰ,Ⅱ,Ⅲ三部分旋转所得几何体的体积之比为 .

答案:
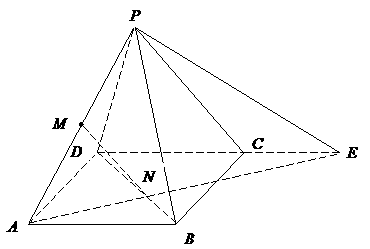
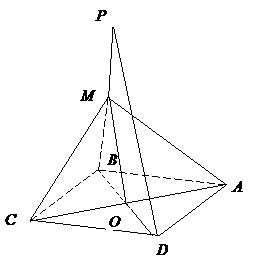
第6题. 如图,正方形 的边长为
的边长为 ,平面
,平面 外一点
外一点 到正方形各顶点的距离都是
到正方形各顶点的距离都是 ,
, ,
, 分别是
分别是 ,
, 上的点,且
上的点,且 .
.
(1)
求证:直线 平面
平面 ;
;
(2)
求线段 的长.
的长.
(1)
答案:证明:连接 并延长交
并延长交 于
于 ,连接
,连接 ,
,
则由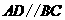 ,得
,得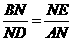 .
.
 ,
, .
.
 ,又
,又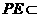 平面
平面 ,
,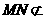 平面
平面 ,
,

 平面
平面 .
.
(2)
解:由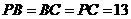 ,得
,得 ;
;
由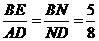 ,知
,知 ,
,
由余弦定理可得 ,
, .
.
第7题. 如图,已知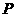 为平行四边形
为平行四边形 所在平面外一点,
所在平面外一点, 为
为 的中点,
的中点,
求证: 平面
平面 .
.

答案:证明:连接 、
、 交点为
交点为 ,连接
,连接 ,则
,则 为
为 的中位线,
的中位线,
 .
.
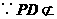 平面
平面 ,
, 平面
平面 ,
,
 平面
平面 .
.
第8题. 如图,在正方体 中,
中,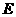 ,
, 分别是棱
分别是棱 ,
, 的中点,求证:
的中点,求证: 平面
平面 .
.

答案:证明:如图,取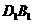 的中点
的中点 ,连接
,连接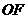 ,
, ,
,
 平行且等于
平行且等于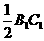 ,
, 平行且等于
平行且等于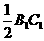 ,
,
 平行且等于
平行且等于 ,则
,则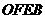 为平行四边形,
为平行四边形,

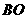 .
.
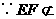 平面
平面 ,
, 平面
平面 ,
,

 平面
平面 .
.

第9题. 如图,在正方体 中,试作出过
中,试作出过 且与直线
且与直线 平行的截面,并说明理由.
平行的截面,并说明理由.

答案:解:如图,连接 交
交 于点
于点 ,取
,取 的中点
的中点 ,连接
,连接 ,
, ,则截面
,则截面 即为所求作的截面.
即为所求作的截面.

 为
为 的中位线,
的中位线,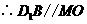 .
.
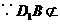 平面
平面 ,
, 平面
平面 ,
,
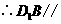 平面
平面 ,则截面
,则截面 为过
为过 且与直线
且与直线 平行的截面.
平行的截面.
第10题. 设 ,
, 是异面直线,
是异面直线, 平面
平面 ,则过
,则过 与
与 平行的平面( )
平行的平面( )
A.不存在 B.有1个
C.可能不存在也可能有1个 D.有2个以上
答案:C.
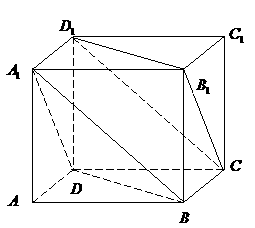
第11题. 如图,在正方体 中,求证:平面
中,求证:平面 平面
平面 .
.
答案:证明:
 四边形
四边形 是平行四边形
是平行四边形



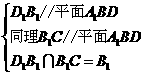

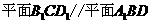 .
.
第12题. 如图, 、
、 、
、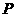 分别为空间四边形
分别为空间四边形 的边
的边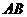 ,
, ,
, 上的点,且
上的点,且 .
.
求证:(1) 平面
平面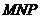 ,
, 平面
平面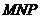 ;
;
(2)平面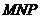 与平面
与平面 的交线
的交线 .
.

答案:证明:(1)
 .
.
 .
.
(2)

 .
.

第13题. 如图,线段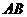 ,
, 所在直线是异面直线,
所在直线是异面直线,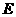 ,
, ,
, ,
, 分别是线段
分别是线段 ,
,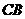 ,
, ,
,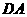 的中点.
的中点.
(1)
求证: 共面且
共面且 面
面 ,
, 面
面 ;
;
(2)
设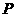 ,
, 分别是
分别是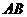 和
和 上任意一点,求证:
上任意一点,求证: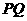 被平面
被平面 平分.
平分.
答案:证明:(1)
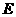 ,
, ,
, ,
, 分别是
分别是 ,
,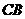 ,
, ,
,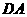 的中点.,
的中点.,
 ,
, ,
, .因此,
.因此,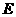 ,
, ,
, ,
, 共面.
共面.
 ,
,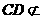 平面
平面 ,
,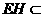 平面
平面 ,
,
 平面
平面 .同理
.同理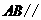 平面
平面 .
.
(2)设 平面
平面 =
= ,连接
,连接 ,设
,设 .
.
 所在平面
所在平面 平面
平面 =
= ,
,
 平面
平面 ,
, 平面
平面 ,
,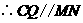 .
.
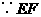 是
是 是的中位线,
是的中位线,
 是
是 的中点,则
的中点,则 是
是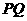 的中点,即
的中点,即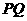 被平面
被平面 平分.
平分.
第14题. 过平面 外的直线
外的直线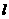 ,作一组平面与
,作一组平面与 相交,如果所得的交线为
相交,如果所得的交线为 ,
, ,
, ,
, ,则这些交线的位置关系为( )
,则这些交线的位置关系为( )
A.都平行
B.都相交且一定交于同一点
C.都相交但不一定交于同一点
D.都平行或都交于同一点
答案:D.
第15题.  ,
, 是两条异面直线,
是两条异面直线, 是不在
是不在 ,
, 上的点,则下列结论成立的是( )
上的点,则下列结论成立的是( )
A.过 且平行于
且平行于 和
和 的平面可能不存在
的平面可能不存在
B.过 有且只有一个平面平行于
有且只有一个平面平行于 和
和
C.过 至少有一个平面平行于
至少有一个平面平行于 和
和
D.过 有无数个平面平行于
有无数个平面平行于 和
和
答案:A.
第16题. 若空间四边形 的两条对角线
的两条对角线 ,
, 的长分别是8,12,过
的长分别是8,12,过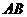 的中点
的中点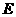 且平行于
且平行于 、
、 的截面四边形的周长为 .
的截面四边形的周长为 .
答案:20.
第17题. 在空间四边形 中,
中,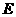 ,
, ,
, ,
, 分别为
分别为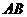 ,
, ,
, ,
,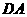 上的一点,且
上的一点,且 为菱形,若
为菱形,若 平面
平面 ,
, 平面
平面 ,
, ,
, ,则
,则 .
.
答案: .
.
第18题. 如图,空间四边形 的对棱
的对棱 、
、 成
成 的角,且
的角,且 ,平行于
,平行于 与
与 的截面分别交
的截面分别交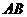 、
、 、
、 、
、 于
于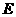 、
、 、
、 、
、 .
.
(1)求证:四边形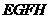 为平行四边形;
为平行四边形;
(2)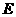 在
在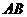 的何处时截面
的何处时截面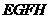 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?
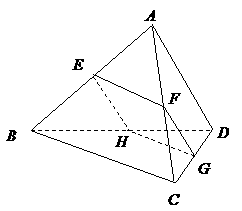
答案:(1)证明: 平面
平面 ,
, 平面
平面 ,
,
平面 平面
平面
 ,
,
 .同理
.同理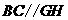 ,
,
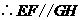 ,同理
,同理 ,
,
 四边形
四边形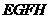 为平行四边形.
为平行四边形.
(2)解:
 与
与 成
成 角,
角,

 或
或 ,设
,设 ,
,
 ,
,
 ,
,
 ,由
,由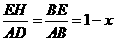 ,
,
得 .
.

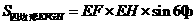
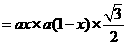
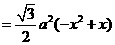
 .
.
当 时,
时,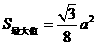 ,
,
即当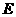 为
为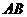 的中点时,截面的面积最大,最大面积为
的中点时,截面的面积最大,最大面积为 .
.
第19题. 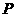 为
为 所在平面外一点,平面
所在平面外一点,平面 平面
平面 ,
, 交线段
交线段 ,
, ,
, 于
于 ,
, ,则
,则 .
.
答案: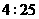
第20题. 如图,在四棱锥 中,
中, 是平行四边形,
是平行四边形, ,
, 分别是
分别是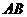 ,
, 的中点.
的中点.
求证: 平面
平面 .
.

答案:证明:如图,取 的中点
的中点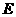 ,连接
,连接 ,
,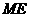

 ,
, 分别是
分别是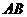 ,
, 的中点,
的中点,
 ,
,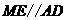 ,
,
可证明 平面
平面 ,
,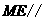 平面
平面 .
.
又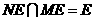 ,
,
 平面
平面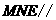 平面
平面 ,
,
又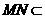 平面
平面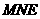 ,
,
 平面
平面 .
.


第21题. 已知平面 平面
平面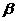 ,
,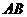 ,
, 是夹在两平行平面间的两条线段,
是夹在两平行平面间的两条线段, ,
, 在
在 内,
内, ,
, 在
在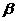 内,点
内,点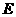 ,
, 分别在
分别在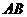 ,
, 上,且
上,且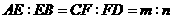 .
.
求证: 平面
平面 .
.
答案:证明:分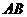 ,
, 是异面、共面两种情况讨论.
是异面、共面两种情况讨论.
(1)
当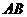 ,
, 共面时,如图(
共面时,如图( )
)
 ,
, ,连接
,连接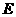 ,
, .
.
 ,
,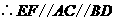 且
且 ,
, ,
,
 平面
平面 .
.


(2)
当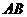 ,
, 异面时,如图(
异面时,如图( ),过点
),过点 作
作
交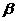 于点
于点 .
.
在 上取点
上取点 ,使
,使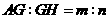 ,连接
,连接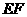 ,由(1)证明可得
,由(1)证明可得 ,又
,又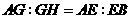 得
得 .
. 平面
平面 平面
平面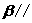 平面
平面 .
.
又 面
面 ,
,
 平面
平面 .
.
第22题. 已知 ,
, ,
,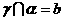 ,且
,且 ,求证:
,求证: .
.
答案:证明:
 .
.

第23题. 三棱锥 中,
中,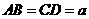 ,截面
,截面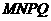 与
与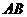 、
、 都平行,则截面
都平行,则截面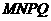 的周长是( ).
的周长是( ).
A.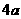 B.
B.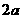
C. D.周长与截面的位置有关
D.周长与截面的位置有关
答案:B.
第24题. 已知: ,
, ,
,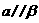 ,则
,则 与
与 的位置关系是( ).
的位置关系是( ).
A. B.
B.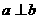
C.试题详情
22.已知 ,
, ,在直线
,在直线 上求一点M,使|MA|+|MB|最小,并求出这个最小值.
上求一点M,使|MA|+|MB|最小,并求出这个最小值.
21.已知直线l1:mx+8y+n=0直线l2:2x+my-1=0, l1 || l2,两平行线间的距为 ,而过点A(m, n)(m>0, n>0)的直线l被l1、l 2截得的线段长为
,而过点A(m, n)(m>0, n>0)的直线l被l1、l 2截得的线段长为 ,求直线l方程.
,求直线l方程.
20. 过点M(0,1)作直线,使它被两已知直线l1: x-3y+10=0和l2:2x+y-8=0所截得的线段恰好被M所平分,求此直线方程.
19.已知直线l满足下列两个条件:
(1)过直线y = – x + 1和y = 2x + 4的交点; (2)与直线x–3y + 2 = 0 垂直,
求直线l的方程.
18.给出下列五个命题:① 过点(–1, 2)的直线方程一定可以表示为y–2=k(x+1);② 过点(–1, 2)且在x轴、y轴截距相等的的直线方程是x+y–1=0; ③ 过点M(–1, 2)且与直线l: Ax+By+C=0(AB≠0)垂直的直线方程是B(x+1)+A(y–2)=0;④ 设点M(–1, 2)不在直线l: Ax+By+C=0(AB≠0)上,则过点M且与l平行的直线方程是A(x+1)+B(y–2)=0; ⑤点P(–1, 2)到直线ax+y+a2+a=0的距离不小于2. 以上命题中,正确的序号是 .
17. 直线ax+by+3=0与直线dx+ey+3=0的交点为(3,–2),则过点(a,b),
(d,e)的直线方程是___________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com