
题目列表(包括答案和解析)
12、解:(1)当 时,
时,


易证 在
在 上是增函数(须证明一下)
上是增函数(须证明一下)

(2)由 有
有 对
对 恒成立
恒成立

令



 即
即
(另有讨论法求和函数最值法求)
11、解:设
(1)
 在
在 上是减函数
上是减函数
 所以值域为
所以值域为
(2)
由
所以 在
在 上是减函数
上是减函数
 或
或 (不合题意舍去)
(不合题意舍去)
当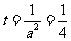 时
时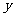 有最大值,
有最大值,
即
10、解:(1)令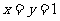 有
有
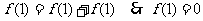
(2)由 有
有 


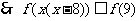
 在
在 上单调递增
上单调递增

即 的取值范围为
的取值范围为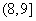
9、解:设甲、乙两种商品的资金投入应分别为 万元,
万元, 万元
万元
则利润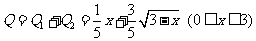
令 则
则



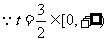
所以当 时,即
时,即 时
时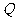 有最大值
有最大值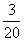
此时 ,
,
则为获最大利润,甲、乙两种商品的资金投入应分别为 万元和
万元和 万元。
万元。
8、解:由已知有 的定义域为
的定义域为 ;
;
(1)当 时,
时, 的值域为
的值域为
当 时,
时,
所以 的值域为
的值域为
(2)

当 即
即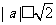 时,
时,


当 即
即 时,
时,

7、解:(1)原式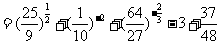

(2)



原式
=

6.(普)(1)当 时,
时, ,
,
所以 时, f(x)的最小值为1;
时, f(x)的最小值为1; 时(x)的最大值为37. ……………6分
时(x)的最大值为37. ……………6分
(2)函数 图象的对称轴为
图象的对称轴为

因为 在区间
在区间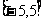 上是单调函数,
上是单调函数,
所以 或
或 ,故
,故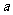 的取值范围是
的取值范围是 或
或 .……………12分
.……………12分
(实)解:(1)∵f(x)是奇函数,∴对定义域内的任意的x,都有 ,
,
即 ,整理得:
,整理得: ∴q=0 ………2分
∴q=0 ………2分
又∵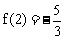 ,∴
,∴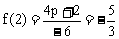 ,
,
解得p=2 …………………………………………4分
∴所求解析式为 …………………………………………5分
…………………………………………5分
(2)由(1)可得 =
= ,
,
设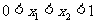 ,
,
则由于
= ………9分
………9分
因此,当 时,
时, ,
,
从而得到 即,
即,
∴ 是f(x)的递增区间。
………………………12分
是f(x)的递增区间。
………………………12分
5.解:设投入甲商品为
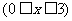 万元,则投入乙商品为
万元,则投入乙商品为 万元,
万元,
总利润为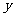 万元 …………………………………………1分
万元 …………………………………………1分
依题意 ………………………………………3分
………………………………………3分
令 …………………………………………4分
…………………………………………4分
因为 ,所以
,所以 ……………………………………5分
……………………………………5分
所以 ……………………………8分
……………………………8分
当 即
即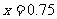 时
时 取最大值
取最大值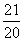 ,此时
,此时 ………………11分
………………11分
答:甲投入0.75万元,乙投入2.25万元时,总共可获得最大利润1.05万元。…12分
4.解:由 ,而
,而 ,
,
当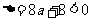 ,即
,即 时,
时,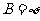 ,符合
,符合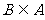 ;
;
当 ,即
,即 时,
时, ,符合
,符合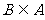 ;
;
当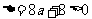 ,即
,即 时,
时, 中有两个元素,而
中有两个元素,而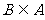
 ;
;
∴ 得
得
∴
3.解,由 ,可得
,可得 或
或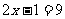 ,解得
,解得 或5。
或5。
当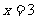 时,
时, ,
, ,集合B中元素违反互异性,故舍去
,集合B中元素违反互异性,故舍去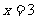 。
。
当 时,
时, ,
,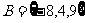 ,满足题意,此时
,满足题意,此时 。
。
当 时,
时, ,
,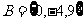 ,此时
,此时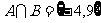 ,这与
,这与 矛盾,故
矛盾,故 舍去。
舍去。
综上知 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com