
题目列表(包括答案和解析)
4.
(A)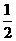 (B)
(B) (C)
(C) (D)
(D)
3.已知角 的终边与单位圆的交点为
的终边与单位圆的交点为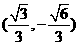 ,则
,则
(A)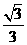 (B)
(B)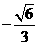 (C)
(C)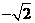 (D)
(D)
2.已知 ,且
,且 ,则
,则 等于
等于
(A) 3
(B) (C)
(C)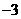 (D)
(D)
1.把一条射线绕着端点按顺时针旋转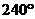 所形成的角是
所形成的角是
(A) (B)
(B)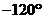 (C)
(C)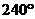 (D)
(D)
13若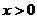 ,
, 且
且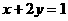 ,则
,则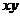 的最大值为___________
的最大值为___________
14设等比数列 的公比
的公比 ,前n项和为
,前n项和为 ,则
,则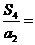 ___________
___________
15设数列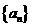 中,
中, ,则通项
,则通项 ___________ 。
___________ 。
16关于函数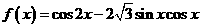 ,下列命题:
,下列命题:
①若存在 ,
,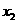 有
有 时,
时, 成立;
成立;
②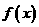 在区间
在区间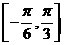 上是单调递增;
上是单调递增;
③函数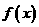 的图像关于点
的图像关于点 成中心对称图像;
成中心对称图像;
④将函数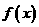 的图像向左平移
的图像向左平移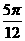 个单位后将与
个单位后将与 的图像重合.
的图像重合.
其中正确的命题序号 (注:把你认为正确的序号都填上)
三解答题:(本大题共6小题,共70分,解答应写出文字说明,证明过程,推演步骤)
17(本小题满分10分)
已知 , 求证:
, 求证: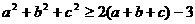
18(本小题满分12分)
已知 .
.
19(本小题满分12分)
已知数列 的前
的前 项和
项和
(1)求数列的通项公式 ;
(2)求 的最大或最小值
的最大或最小值
20(本小题满分12分)
已知 、
、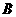 、
、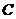 为
为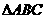 的三内角,且其对边分别为
的三内角,且其对边分别为 、
、 、
、 ,若
,若
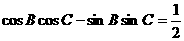 .
.
(Ⅰ)求 ;
;
(Ⅱ)若 ,求
,求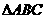 的面积.
的面积.
21(本小题满分12分)
某房地产开发商投资81万元建一座写字楼,第一年装修费为1万元,以后每年增加2万
元,把写字楼出租,每年收入租金30万元.
(Ⅰ)若扣除投资和各种装修费,则从第几年开始获取纯利润?
(Ⅱ)若干年后开发商为了投资其他项目,有两种处理方案:①年平均利润最大时以
46万元出售该楼; ②纯利润总和最大时,以10万元出售该楼,问哪种方案
盈利更多?
22(本小题满分12分)
数列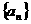 的各项均为正数,
的各项均为正数,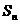 为其前n项和,对于任意
为其前n项和,对于任意 ,总有
,总有 ,
,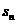 ,
, 成
成
等差数列。
(1)求数列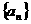 的通项公式;
的通项公式;
(2)设 ,其前n项和是
,其前n项和是 ,求证:
,求证: 。
。
20.(本小题满分16分)
已知等比数列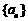 的公比为
的公比为 ,首项为
,首项为 ,其前
,其前 项的和为
项的和为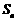 .数列
.数列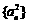 的前
的前 项的和为
项的和为 , 数列
, 数列 的前
的前 项的和为
项的和为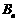 .
.
(1)若 ,
,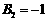 ,求
,求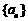 的通项公式;
的通项公式;
(2)①当 为奇数时,比较
为奇数时,比较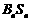 与
与 的大小;
的大小;
②当 为偶数时,若
为偶数时,若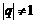 ,问是否存在常数
,问是否存在常数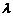 (与n无关),使得等式
(与n无关),使得等式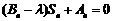 恒
恒
成立,若存在,求出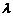 的值;若不存在,说明理由.
的值;若不存在,说明理由.

19.(本小题满分16分)
如图 中,已知点
中,已知点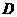 为
为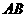 边中点,点
边中点,点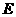 为
为 边靠近点
边靠近点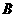 的三等分点,点
的三等分点,点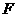 是
是 上一点,且满足
上一点,且满足 ,记
,记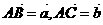 .
.
(1)用 表示
表示 ;(2)求证:
;(2)求证: 三点共线;
三点共线;
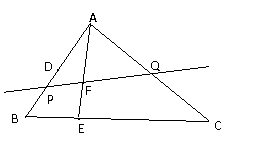 (3)过点
(3)过点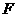 作直线
作直线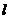 与
与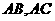 分别交于点
分别交于点 .设
.设 (
( ).
).
求证: .
.
18.(本小题满分15分)
设 的内角
的内角 所对的边长分别为
所对的边长分别为 ,且
,且 ,
, .
.
(1)求 的值;(2)求边长
的值;(2)求边长 ;
;
(3)若 的面积
的面积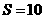 ,求
,求 的值.
的值.
17.(本小题满分15分)
已知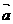 、
、 、
、 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中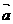 =(1,2).
=(1,2).
⑴若|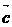 |
| ,且
,且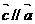 ,求
,求 的坐标;
的坐标;
⑵若| |=
|= 且
且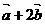 与
与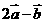 垂直,求
垂直,求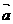 与
与 的夹角
的夹角 .
.
16.(本小题满分14分)
已知等差数列{ }的前n项和为
}的前n项和为 ,且
,且 =5,
=5, =225.
=225.
(1)求数列{ }的通项
}的通项 ;
;
(2)设 ,求数列
,求数列 的前n项和
的前n项和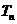 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com