3.　　　 “和定积最大，积定和最小，”即2个正数的和为定值，则可求其积的最大值；积为定值，则可求其和的最小值。

应用此结论求值要注意三个条件：

⑴各项或因式非负；

⑵和或积为定值；　　　　　　　　　　　 一正二定三相等

⑶等号能不能取到。

　 必要时要作适当的变形，以满足上述前提。

例1、若x<0，则2 + 3x + 的最大值是　　　 (　 )

　(A) 2 + 4　　 (B) 2±4 (C) 2－4 (D) 以上都不对

例2、已知x，y都是正数，且，求x+y的最小值。

例3、已知a>b>0，则a² + 的最小值是_________。

巩固练习

2.　　　 创设应用均值不等式的条件、合理拆分项或配凑因式是常用的解题技巧，而拆与凑的成因在于使等号能够成立。

1.　　　 二元均值不等式具有将“和式”转化为“积式”和“积式”转化为“和式”的放缩功能。

21．当矩形温室的边长的左右长为20m，前后长为40m时，种植面积最大，最大种植面积为648m².

版权所有：()

版权所有：()

20．

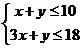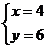解：，设　　　 当时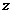，取最大值7万元

19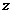．的最大值为13，此时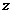；的最小值为，此时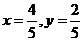

18．

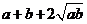
17．略

16．3

15．18