
题目列表(包括答案和解析)
5、3.在△ABC中,AB=AC,D、E分别是AB、AC的中点,则 ( )
A. 与
与 共线
B.
共线
B. 与
与 共线
共线
C.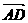 与
与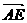 相等
D.
相等
D.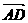 与
与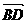 相等
相等
4、下列四个函数中,在(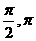 )上为增函数的是( )
)上为增函数的是( )
A.y=cosx B.y=cos2x C.y=sinx D.y=sin2x
3、函数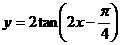 的定义域是( )
的定义域是( )
A.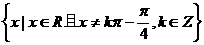 B.
B.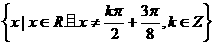
C.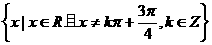 D.
D.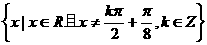
2、下列函数中,最小正周期为 的是( )
的是( )
A.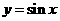 B.
B. C.
C.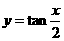 D.
D.
1、 化为弧度是( )
化为弧度是( )
A. 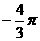 B.
B. 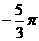 C.
C. 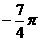 D.
D. 
22.解析:设符合条件的正多边形的边数分别为m、n(m、n≥3,且m、n∈N)
则它们对应的正多边形的内角分别为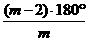 和
和 rad
rad
据题意: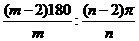 =144∶π
=144∶π
∴ ×144=
×144=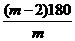 ×π,∴4(1-
×π,∴4(1-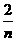 )=5(1-
)=5(1-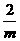 )
)
4-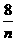 =5-
=5-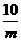 ,
,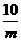 =1+
=1+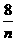 ,
,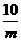 =
= ,
, =
=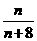
m=10(1-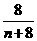 )=10-
)=10-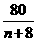
∵m∈N,∴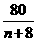 是自然数,n+8是80的约数.
是自然数,n+8是80的约数.
∵m≥3,∴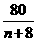 ≤7,∴n+8≥
≤7,∴n+8≥
又n≥3,且n+8是80的约数. ∴n+8可取16、20、40、80.
当n+8=16时,n=8,m=5; 当n+8=20时,n=12,m=6;
当n+8=40时,n=32,m=8; 当n+8=80时,n=72,m=9;
故所求的正多边形有四组,分别是
正五边形和正八边形. 正六边形和正十二边形.
正八边形和正三十二边形. 正九边形和正七十二边形.
21.解析: .
.
20.解析:由于大链轮与小链轮在相同时间内转过的齿数相同,所以两轮转过的圈数之比与它们的齿数成反比,于是大轮转过的圈数:小转轮过的圈数=20∶48
据此解得当大轮转1周时,小轮转2.4周.
故小轮转过的角度为360°×2.4=864°
小轮转过的弧度为864°× rad.
rad.
答:当大链轮转过一周时,小链轮转过的角度是864°,弧度是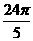 rad.
rad.
19.解析:设扇形的半径为R,弧长为l,面积为S
∵c=2R+l,∴R=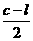 (l<c)
(l<c)
则S=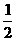 Rl=
Rl=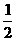 ×
×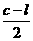 ·l=
·l=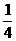 (cl-l2)=-
(cl-l2)=-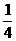 (l2-cl)=-
(l2-cl)=-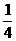 (l-
(l-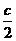 )2+
)2+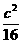
∴当l=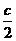 时,Smax=
时,Smax=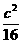
答:当扇形的弧长为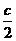 时,扇形有最大面积,扇形面积的最大值是
时,扇形有最大面积,扇形面积的最大值是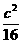 .
.
18.解析:∵A、B、C成等差数列,∴A+C=2B
又A+B+C=π,∴3B=π,∴B=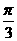 ,A+C=
,A+C=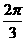
又A-C=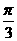 ,∴A=
,∴A=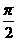 ,C=
,C=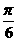
∴cos2A+cos2B+cos2C=cos2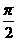 +cos2
+cos2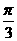 +cos2
+cos2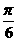 =0+
=0+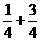 =1.
=1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com