
题目列表(包括答案和解析)
3、若动直线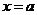 与函数
与函数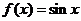 和
和 的图像分别交于
的图像分别交于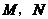 两点,则
两点,则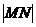 的最大值为( )
的最大值为( )
A、1 B、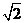 C、
C、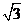 D、2
D、2
2、设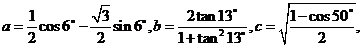 则有( )
则有( )
A、 B、
B、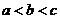 C、
C、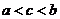 D、
D、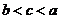
1、已知 则
则 的值为 ( )
的值为 ( )
A、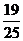 B、
B、 C、
C、 D、
D、
22.解析:设直角三角形的两个锐角分别为α、β,则可得α+β= ,
,
∴cosα=sinβ
∵方程4x2-2(m+1)x+m=0中,Δ=4(m+1)2-4·4m=4(m-1)2≥0
∴当m∈R,方程恒有两实根.
又∵cosα+cosβ=sinβ+cosβ=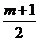 ,cosα·cosβ=sinβcosβ=
,cosα·cosβ=sinβcosβ=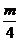
∴由以上两式及sin2β+cos2β=1,得1+2·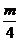 =(
=(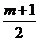 )2
)2
解得m=±
当m= 时,cosα+cosβ=
时,cosα+cosβ=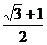 >0,cosα·cosβ=
>0,cosα·cosβ=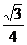 >0,满足题意,
>0,满足题意,
当m=- 时,cosα+cosβ=
时,cosα+cosβ=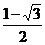 <0,这与α、β是锐角矛盾,应舍去.
<0,这与α、β是锐角矛盾,应舍去.
综上,m=
21.解析:∵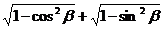 =
= =|sinβ|+|cosβ|=sinβ-cosβ
=|sinβ|+|cosβ|=sinβ-cosβ
∴sinβ≥0,cosβ≤0
∴β是第二象限角或终边在x轴负半轴和y轴正半轴上的角
∵0≤β≤2π,∴ ≤β≤π
≤β≤π
20.解析:原式= ·
·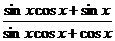
=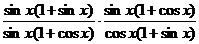 =
=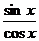 =tanx
=tanx
19.解析:设P(m,-3m)是θ终边上任一点,则
r= |m|
|m|
当m>0时,r= m.
m.
∴sinθ=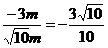 , secθ=
, secθ=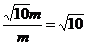
∴10sinθ+3secθ=-3 =0
=0
当m<0时,r=- m, ∴sinθ=
m, ∴sinθ=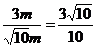 ,secθ=
,secθ=
∴10sinθ+3secθ=3 =0
=0
综上,得10sinθ+3secθ=0
18. 解析: (Ⅰ)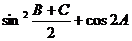
=
= =
= =
= 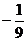
(Ⅱ) ∵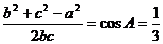
∴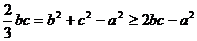 , 又∵
, 又∵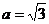 ∴
∴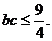
当且仅当 b=c=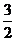 时,bc=
时,bc=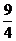 ,故bc的最大值是
,故bc的最大值是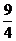 .
.
17.解析:∵sinθ+cosθ=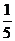 ,(1)
,(1)
将其平方得,1+2sinθcosθ=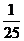 ,∴2sinθcosθ=-
,∴2sinθcosθ=-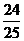 ,
,
∵θ∈(0,π), ∴cosθ<0<sinθ
∵(sinθ-cosθ)2=1-2sinθcosθ=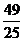 , ∴sinθ-cosθ=
, ∴sinθ-cosθ=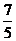 (2)
(2)
由(1)(2)得sinθ= ,cosθ=-
,cosθ=-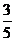 ,∴cotθ=
,∴cotθ=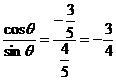 .
.
13.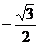 14.{x|x≠
14.{x|x≠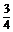 π+kπ,k∈Z} 15.
π+kπ,k∈Z} 15. 16.0
16.0
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com