
题目列表(包括答案和解析)
4、下列命题中正确的是( )
A. 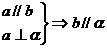 B.
B.

C.  D.
D.

3、已知直线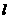 ∥平面
∥平面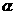 ,直线
,直线 ,则
,则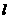 与
与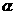 必定( )
必定( )
A.平行 B.异面 C.相交 D.无公共点
2、若 ∥
∥ ,
, ,则
,则 的位置关系是( )
的位置关系是( )
A.异面直线 B.相交直线
C.平行直线 D.相交直线或异面直线
1、下列命题,真命题的是( )
A.空间不同的三点确定一个平面
B.空间两两相交的三条直线确定一个平面
C.和同一直线都相交的三条平行线在同一平面内
D.两组对边相等的四边形是平行四边形
15.(本题满分7分)某工厂生产甲、乙两种产品.甲产品的一等品率为80%,二等品率为20%;乙产品的一等品率为90%,二等品率为10%.生产1件甲产品若是一等品则获利4万元,若是二等品则亏损1万元;生产1件乙产品若是一等品则获利6万元,若是二等品则亏损2万元.设生产各件产品相互独立.
(1)记X(单位:万元)为生产1件甲产品和1件乙产品可获得的总利润,求X的分布列;
(2)求生产4件甲产品所获得的总利润不少于10万元的概率.
解:(1)由题设知X的可能取值为10,5,2,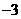 .且
.且
 ,
,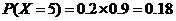 ,
,
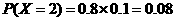 ,
, 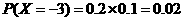 .
.
由此得X的分布列为
|
X |
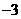 |
2 |
5 |
10 |
|
P |
0.02 |
0.08 |
0.18 |
0.72 |
(2)设生产的4件甲产品中一等品n件,则二等品有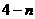 件.
件.
由题设知 解得
解得 .
.
又
所以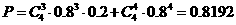
 所求概率为0.8192
所求概率为0.8192
14.(本题满分7分)甲乙两人独立解某一道数学题,已知该题被甲独立解出的概率为0.6,被甲或乙解出的概率为0.92.
(1)求该题被乙独立解出的概率;
(2)求解出该题的人数 的数学期望和方差
的数学期望和方差
解:(1)记甲、乙分别解出此题的事件记为A、B.
设甲独立解出此题的概率为P1,乙为P2.
则P(A)=P1=0.6,P(B)=P2

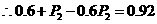

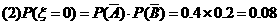
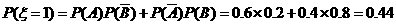
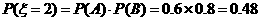

 |
0 |
1 |
2 |
|
P |
0.08 |
0.44 |
0.48 |
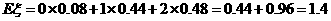



13. (本题满分6分)从8名运动员中选出4人参加 接力赛,分别求满足下列条件的安排方法种数:
接力赛,分别求满足下列条件的安排方法种数:
(1)甲、乙两人都不跑中间两棒;
(2)甲、乙二人不都跑中间两棒.
解:(1)先选跑中间的两人有 种,再从余下的6人中选跑1、4棒的有
种,再从余下的6人中选跑1、4棒的有 ,则共有
,则共有 种.
种.
(2)用间接法:“不都跑”的否定是“都跑”,所以用任意排法 ,再去掉甲、乙跑中间的安排方法
,再去掉甲、乙跑中间的安排方法 种,它们的差是1620种.
种,它们的差是1620种.
12.(本题满分5分)设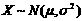 ,且总体密度曲线的函数表达式为:
,且总体密度曲线的函数表达式为: ,x∈R.
,x∈R.
(1)求m,s;
(2)求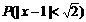 的值.
的值.
以下数据供选用: ,
,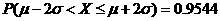

解:(1)由于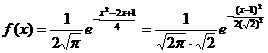 ,
,
根据一般正态分布的函数表达形式,可知μ=1,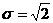 ,故X-N(1,2).
,故X-N(1,2).
(2)

11.(本题满分5分)已知 的展开式中的前三项系数成等差数列,求展开式中含
的展开式中的前三项系数成等差数列,求展开式中含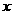 的项的系数.
的项的系数.
解:因为 ,故前三
,故前三
项的系数分别为1, ,
,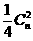 .依题意:
.依题意:
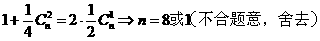

10. 已知随机变量 服从二项分布
服从二项分布 ,则P(
,则P( =2) =
( ) D
=2) =
( ) D
A. 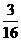 B.
B.  C.
C.
 D.
D. 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com