
题目列表(包括答案和解析)
7.如果正数 满足
满足 ,那么
( )
,那么
( )
A. ,且等号成立时
,且等号成立时 的取值唯一
的取值唯一
B. ,且等号成立时
,且等号成立时 的取值唯一
的取值唯一
C. ,且等号成立时
,且等号成立时 的取值不唯一
的取值不唯一
D. ,且等号成立时
,且等号成立时 的取值不唯一
的取值不唯一
6.已知a、b、m是正实数,则不等式 ( )
( )
A.当a> b时成立 B.当a< b时成立
C.是否成立与m有关 D.一定成立
5.设 ,则x,y的大小是
( )
,则x,y的大小是
( )
A. B.
B. C.
C. D.与m,n的取值有关
D.与m,n的取值有关
4.下列函数中最小值是2的是 ( )
A. B.
B.
C.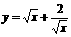 D.
D. ×
×
3.在
 ①
① , ②
, ② ③
③ ,
,
其中正确的个数是 ( )
A.0 B.1 C.2 D.3
2.综合法证明不等式中所说的“由因导果”是指寻求使不等式成立的 ( )
A.必要条件 B.充分条件 C.充要条件 D.必要或充分条件
1.四个不相等的正数a,b,c,d成等差数列,则 ( )
A. B.
B. C.
C.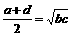 D.
D.
2、放缩法一般包括:用缩小分母,扩大分子,分式值增大;缩小分子,扩大分母,分式值缩小;全量不少于部分;每一次缩小其和变小,但需大于所求,第一次扩大其和变大,但需小于所求,即不能放缩不够或放缩过头,同时放缩后便于求和.
典型例题十一
例11 已知 ,求证:
,求证: .
.
分析:欲证不等式看起来较为“复杂”,宜将它化为较“简单”的形式,因而用分析法证明较好.
证明:欲证 ,
,
只须证 .
.
即要证 ,
,
即要证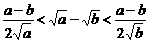 .
.
即要证 ,
,
即要证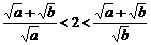 .
.
即要证 ,即
,即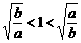 .
.
即要证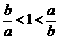 (*)
(*)
∵ ,∴(*)显然成立,
,∴(*)显然成立,
故
说明:分析法证明不等式,实质上是寻求结论成立的一个充分条件.分析法通常采用“欲证--只要证--即证--已知”的格式.
典型例题十二
例12 如果 ,
, ,
,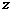
 ,求证:
,求证: .
.
分析:注意到不等式左边各字母在项中的分布处于分离状态,而右边却结合在一起,因而要寻求一个熟知的不等式具有这种转换功能(保持两边项数相同),由 ,易得
,易得 ,此式的外形特征符合要求,因此,我们用如下的结合法证明.
,此式的外形特征符合要求,因此,我们用如下的结合法证明.
证明:∵
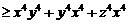
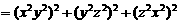
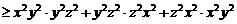
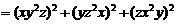

 .
.
∴ .
.
说明:分析时也可以认为是连续应用基本不等式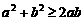 而得到的.左右两边都是三项,实质上是
而得到的.左右两边都是三项,实质上是 公式的连续使用.
公式的连续使用.
如果原题限定 ,
, ,
,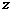
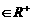 ,则不等式可作如下变形:
,则不等式可作如下变形: 进一步可得到:
进一步可得到: .
.
显然其证明过程仍然可套用原题的思路,但比原题要难,因为发现思路还要有一个转化的过程.
典型例题十三
例13 已知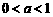 ,
, ,
, ,求证:在
,求证:在 三数中,不可能都大于
三数中,不可能都大于 .
.
分析:此命题的形式为否定式,宜采用反证法证明.假设命题不成立,则 三数都大于
三数都大于 ,从这个结论出发,进一步去导出矛盾.
,从这个结论出发,进一步去导出矛盾.
证明:假设 三数都大于
三数都大于 ,
,
即 ,
,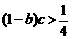 ,
, .
.
又∵ ,
,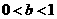 ,
, ,
,
∴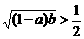 ,
,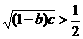 ,
, .
.
∴ ①
①
又∵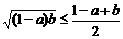 ,
, ,
, .
.
以上三式相加,即得:
 ②
②
显然①与②相矛盾,假设不成立,故命题获证.
说明:一般情况下,如果命题中有“至多”、“至少”、“都”等字样,通常情况下要用反证法,反证法的关键在于“归谬”,同时,在反证法的证明过程中,也贯穿了分析法和综合法的解题思想.
典型例题十四
例14 已知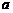 、
、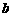 、
、 都是正数,求证:
都是正数,求证: .
.
分析:用分析法去找一找证题的突破口.要证原不等式,只需证 ,即只需证
,即只需证 .把
.把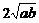 变为
变为 ,问题就解决了.或有分析法的途径,也很容易用综合法的形式写出证明过程.
,问题就解决了.或有分析法的途径,也很容易用综合法的形式写出证明过程.
证法一:要证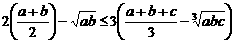 ,
,
只需证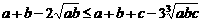 ,
,
即 ,移项,得
,移项,得 .
.
由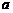 、
、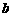 、
、 为正数,得
为正数,得 .
.
∴原不等式成立.
证法二:∵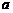 、
、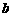 、
、 为正数,
为正数,
 .
.
即 ,故
,故 .
.
 ,
,
 .
.
说明:题中给出的 ,
, ,
, ,
,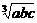 ,只因为
,只因为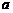 、
、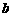 、
、 都是正数,形式同算术平均数与几何平均数定理一样,不加分析就用算术平均数与几何平均数定理来求证,问题就不好解决了.
都是正数,形式同算术平均数与几何平均数定理一样,不加分析就用算术平均数与几何平均数定理来求证,问题就不好解决了.
原不等式中是用“不大于”连结,应该知道取等号的条件,本题当且仅当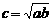 时取“=”号.证明不等式不论采用何种方法,仅仅是一个手段或形式问题,我们必须掌握证题的关键.本题的关键是证明
时取“=”号.证明不等式不论采用何种方法,仅仅是一个手段或形式问题,我们必须掌握证题的关键.本题的关键是证明 .
.
典型例题十五
例15 已知 ,
,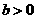 ,且
,且 .求证:
.求证: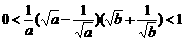 .
.
分析:记 ,欲证
,欲证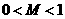 ,联想到正、余弦函数的值域,本题采用三角换元,借助三角函数的变换手段将很方便,由条件
,联想到正、余弦函数的值域,本题采用三角换元,借助三角函数的变换手段将很方便,由条件 ,
,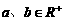 可换元,围绕公式
可换元,围绕公式 来进行.
来进行.
证明:令 ,
, ,且
,且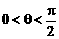 ,
,
则

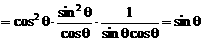
∵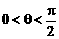 ,∴
,∴ ,即
,即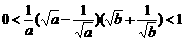 成立.
成立.
说明:换元的思想随处可见,这里用的是三角代换法,这种代换如能将其几何意义挖掘出来,对代换实质的认识将会深刻得多,常用的换元法有:(1)若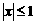 ,可设
,可设 ;(2)若
;(2)若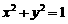 ,可设
,可设 ,
, ,
, ;(3)若
;(3)若 ,可设
,可设 ,
,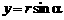 ,且
,且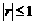 .
.
典型例题十六
例16 已知 是不等于1的正数,
是不等于1的正数, 是正整数,求证
是正整数,求证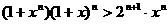 .
.
分析:从求证的不等式看,左边是两项式的积,且各项均为正,右边有2的因子,因此可考虑使用均值不等式.
证明:∵ 是不等于1的正数,
是不等于1的正数,
∴ ,
,
∴ . ①
. ①
又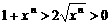 . ②
. ②
将式①,②两边分别相乘得
 ,
,
∴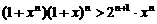 .
.
说明:本题看起来很复杂,但根据题中特点,选择综合法求证非常顺利.由特点选方法是解题的关键,这里因为 ,所以等号不成立,又因为①,②两个不等式两边均为正,所以可利用不等式的同向乘性证得结果.这也是今后解题中要注意的问题.
,所以等号不成立,又因为①,②两个不等式两边均为正,所以可利用不等式的同向乘性证得结果.这也是今后解题中要注意的问题.
典型例题十七
例17 已知, ,
, ,
,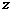
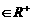 ,且
,且 ,求证
,求证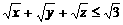 .
.
分析:从本题结构和特点看,使用比较法和综合法都难以奏效.为找出使不等式成立的充分条件不妨先用分析法一试,待思路清晰后,再决定证题方法.
证明:要证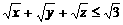 ,
,
只需证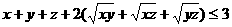 ,
,
只需证 .
.
∵ ,
, ,
,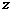
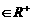 ,
,
∴ ,
, ,
,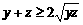 ,
,
∴ ,
,
∴ 成立.
成立.
∴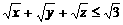 .
.
说明:此题若一味地用分析法去做,难以得到结果.在题中得到只需证 后,思路已较清晰,这时改用综合法,是一种好的做法.通过此例可以看出,用分析法寻求不等式的证明途径时,有时还要与比较法、综合法等结合运用,决不可把某种方法看成是孤立的.
后,思路已较清晰,这时改用综合法,是一种好的做法.通过此例可以看出,用分析法寻求不等式的证明途径时,有时还要与比较法、综合法等结合运用,决不可把某种方法看成是孤立的.
典型例题十八
例18 求证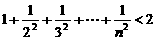 .
.
分析:此题的难度在于,所求证不等式的左端有多项和且难以合并,右边只有一项.注意到这是一个严格不等式,为了左边的合并需要考查左边的式子是否有规律,这只需从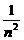 下手考查即可.
下手考查即可.
证明:∵ ,
,
∴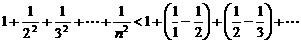
 .
.
说明:此题证明过程并不复杂,但思路难寻.本题所采用的方法也是解不等式时常用的一种方法,即放缩法.这类题目灵活多样,需要巧妙变形,问题才能化隐为显,这里变形的这一步极为关键.
典型例题十九
例19 在 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为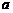 ,
,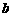 ,
, ,若
,若 ,求证
,求证 .
.
分析:因为涉及到三角形的边角关系,故可用正弦定理或余弦定理进行边角的转化.
证明:∵ ,∴
,∴ .
.
由余弦定理得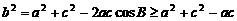
∴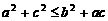 ,
,
∴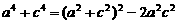
=



说明:三角形中最常使用的两个定理就是正弦和余弦定理,另外还有面积公式 .本题应用知识较为丰富,变形较多.这种综合、变形能力需要读者在平时解题时体会和总结,证明不等式的能力和直觉需要长期培养.
.本题应用知识较为丰富,变形较多.这种综合、变形能力需要读者在平时解题时体会和总结,证明不等式的能力和直觉需要长期培养.
2.用分析法证明数学问题,要求相邻两步的关系是 ,前一步是后一步的必要条件,后一步是前一步的充分条件,当然相互为充要条件也可以.
,前一步是后一步的必要条件,后一步是前一步的充分条件,当然相互为充要条件也可以.
典型例题九
例9 已知 ,求证
,求证 .
.
分析:联想三角函数知识,进行三角换元,然后利用三角函数的值域进行证明.
证明:从条件看,可用三角代换,但需要引入半径参数 .
.
∵ ,
,
∴可设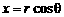 ,
,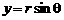 ,其中
,其中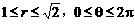 .
.
∴ .
.
由 ,故
,故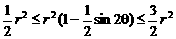 .
.
而 ,
, ,故
,故 .
.
说明:1.三角代换是最常见的变量代换,当条件为 或
或 或
或 时,均可用三角代换.2.用换元法一定要注意新元的范围,否则所证不等式的变量和取值的变化会影响其结果的正确性.
时,均可用三角代换.2.用换元法一定要注意新元的范围,否则所证不等式的变量和取值的变化会影响其结果的正确性.
典型例题十
例10 设 是正整数,求证
是正整数,求证 .
.
分析:要求一个 项分式
项分式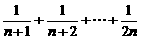 的范围,它的和又求不出来,可以采用“化整为零”的方法,观察每一项的范围,再求整体的范围.
的范围,它的和又求不出来,可以采用“化整为零”的方法,观察每一项的范围,再求整体的范围.
证明:由 ,得
,得 .
.
当 时,
时, ;
;
当 时,
时,
……
当 时,
时, .
.
∴ .
.
说明:1、用放缩法证明不等式,放缩要适应,否则会走入困境.例如证明 .由
.由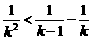 ,如果从第3项开始放缩,正好可证明;如果从第2项放缩,可得小于2.当放缩方式不同,结果也在变化.
,如果从第3项开始放缩,正好可证明;如果从第2项放缩,可得小于2.当放缩方式不同,结果也在变化.
11、1/15 13、(1)9/28 (2)1/28
欢迎访问“俊秀之家”
[高&考%资(源#网]


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com