
题目列表(包括答案和解析)
8.正六棱台的两底边长分别为1cm,2cm,高是1cm,它的侧面积为 ( )
A.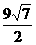 cm2 B.
cm2 B.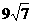 cm2 C.
cm2 C.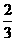
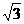 cm2 D.3
cm2 D.3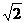 cm2
cm2
7.下列四个说法
①a//α,b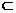 α,则a//
b ②a∩α=P,b
α,则a//
b ②a∩α=P,b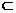 α,则a与b不平行
α,则a与b不平行
③a α,则a//α ④a//α,b
//α,则a//
b
α,则a//α ④a//α,b
//α,则a//
b
其中错误的说法的个数是 ( )
A.1个 B.2个 C.3个 D.4个
6.如图所示,用符号语言可表达为( )
A.α∩β=m,n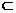 α,m∩n=A
α,m∩n=A
B.α∩β=m,n∈α,m∩n=A
C.α∩β=m,n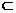 α,A
α,A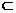 m,A
m,A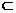 n
n
D.α∩β=m,n∈α,A∈m,A∈ n
5.已知直线a、b与平面α、β、γ,下列条件中能推出α∥β的是 ( )
A.a⊥α且a⊥β B.α⊥γ且β⊥γ
C.a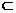 α,b
α,b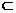 β,a∥b D.a
β,a∥b D.a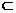 α,b
α,b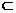 α,a∥β,b∥β
α,a∥β,b∥β
4.若一个平行六面体的四个侧面都是正方形,则这个平行六面体是 ( )
A.正方体 B.正四棱锥 C.长方体 D.直平行六面体
3.棱台上下底面面积分别为16和81,有一平行于底面的截面面积为36,则截面戴的两棱台高
的比为 ( )
A.1∶1 B.1∶1 C.2∶3 D.3∶4
2.利用斜二测画法得到的
①三角形的直观图一定是三角形;
②正方形的直观图一定是菱形;
③等腰梯形的直观图可以是平行四边形;
④菱形的直观图一定是菱形.
以上结论正确的是 ( )
A.①② B. ① C.③④ D. ①②③④
1.不共面的四点可以确定平面的个数为 ( )
A. 2个 B. 3个 C. 4个 D.无法确定
4.在正方体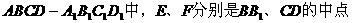
 (1)证明:
(1)证明: ;
;
(2)求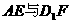 所成的角;
所成的角;
(3)证明: .
.
 1.长方体ABCD-A1B1C1D1中被截去一部分,其中EF∥A1D1.剩下的几何体是什么?截取的几何体是什么?若FH∥EG,但FH<EG,截取的几何体是什么?
1.长方体ABCD-A1B1C1D1中被截去一部分,其中EF∥A1D1.剩下的几何体是什么?截取的几何体是什么?若FH∥EG,但FH<EG,截取的几何体是什么?
2.正四棱台的高,侧棱,对角线长分别为7cm,9cm,11cm,求它的侧面积.
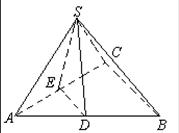 3.三棱锥S-ABC的三条侧棱两两垂直,SA=5,SB=4,SC=3,D为AB中点,E为AC中点,求四棱锥S-BCED的体积.
3.三棱锥S-ABC的三条侧棱两两垂直,SA=5,SB=4,SC=3,D为AB中点,E为AC中点,求四棱锥S-BCED的体积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com